Compendi de l'art de l'algorisme

En nom de nostre senhor dieus Jesus christ, misericordios et piatados, vertadier dieu et vertadier home, al qual non ha par, et de la sua beneseta mayre la gloriosa verges maria, avocada dels crestians, e de mons. sant anthoni, martir, capitani governador et deffendedor de la universitat et comuna de la ciutat de pamias, qui cum patre et filio et spiritui sancto vivit et regnat per infinita secula seculorum amen .

* Abū ʿAbdallāh Muḥammad ibn Mūsā al-Khwārizmī, matematic, geograf, astrològ e astronòm persan (780-850) Acomensa un breu compendi de l'art de l'algorisme^* que foc natural de vida, et foc trop savi home et discret et maystre en quatre sciencias. So es en arismetica geometria musica et astronomia. E ell vesent et aprop entendent que l'art de astronomia era manuscrich: er tota formada e era radicada  en contes e non podia esser entenduda sens cognoyssement de contes. Per so trobec maniera et art per lo qual cascun pot breument compendre e ajustar tota manieyra de contes los quals contes son departis en 5 manieyras. La premieras appellada aplegament. La segonda substractio. La 3 ajustament. La 4 duplacio.

La 5^ta multiplicatio. La 6^ta devisio. La 7^na radicum extractio. La 8^na dels nombres infractio.

Et premierament com assaber que manuscrich: es causas son e que vol dire conte.

Conte es e vol dire aytant como aplegament de unitatz. O anquaras aplegament de diversas unitatz e es partit en tropas mutas.

Aquest art que se segueis foc treyt del algorisme e fa se per 10 figuras las quals son aquestas 0987654321.

Aquestas figuras se contan a la part esquerra. Car al loc ont se pausa la 1 es appellada la premiera et la 2 al segont e la 3 al tertz e aixi seguent per orde. Et la premiera figura vol dire un. La segonda dus. La terza tres. Et aixi meteys de las autras entro a la derrieyra. La qual es appellada chifra. Car la chifra non significa res mas fa significar a las autras.

Que significa cada figura.

Tota figura pausada al premier loc significa si meteyssa. Et al segont loc talas 10 com es lo premier loc. e al tertz loc talas 10 com son al segont loc e en lo quart loc talas 10 com son al tertz loc. E aixi en anant en los autres lox per orde en manierra que la derrieyra figura mas significara que totas las autras figuras.

Quantas manieyras hy a de contes.

Sapias que 3 manieyras hi a de contes, so es dit, article et nombre conpost ; dit es appellat entro a 10; article son appelladas las 10^nas; Nombre compost son de articles et de ditz. Per so sapias que si era una figura sola es dit. E si 2 figuras o mais hi avia, la premiera sera figura significant tant quant seran las figuras compostas. E aixi lo dit se met al premier loc e la figura detras so es la chifra. E sera appellat article. E si es nombre compost premierament pausa lo dit aprop l'article. E si la premiera letra sera par pertot lo conte sera par. Si la premiera letra sera non par, tot lo conte sera non par.

Per so deves saber que cascuna causa per si particularment a devesit per lo nombre de tres tresque perfieytament. Per raso de totas sas partidas las quals totas ensemps lo reddon perfieytament sens mais ni sens mens conte perfieyt la qual perfectio non se pot atrobar en dengun autre nombre.

Et lo dit compendi aura tres partidas principals. La premiera tractara de nombre entier.

E la 2^a que deyssent de la premiera dara la cognoyssensa del nombre rot.

E la 3^a que procedis de las 2 premieras ensenhara de respondre a las questions e rasons que se fan en nombres.

E car lo nombre de 3 es lo premier nombre perfieyt per raso de sas partidas en las quals se pot partir engoalment las quals totas ensemps lo redden perfieyt lo

nombre entier complidament en 6 capitols sera contengut en aquest present compendi.

Dels lo premier ensenhara de contar tot nombre.

Lo 2 demostrara de ajustar diverses nombres en un nombre.

Lo 3 dira la manieyra de sostrayre un nombre de un autre.

Lo 4 dara la practica de multiplicar. Lo 5 dara la cognoyssensa de partir.

Lo 6 sera per saber trayre la raditz dels nombres entiers. e es be de notar que tres capitols d'aquels si es en la practica son contraris dels autres tres.

Car ajustar sustrayre e multiplicar acomensan a la man dreyta. E contar partir trayre la raditz acomensan a la part esquerra [sic].

[1] Premierament es a saber que vol dire contar

Contar es lo nombre prepausat en alcunas figuras comunas de paraulla perceptiblament expremir.

Autrament contar es lo nombre en l’entendement conceuput per figuras comunas vesiblament representar ho de paraulla perceptiblament expremir.

E deves saber que aixi com lo nombre de 10 es lo premier nombre complit. lo qual nombre en si totz los nombres que son que passan 10 non son si no diversas vegadas dire o repetir 10 o 30 que es contengut de dins. 10 o lo cascun e aixi non son si non 10 figuras

comunas ab las quals diversas vegadas retornadas tot nombre se pot escriure las quals comunament se appellan chifras. mas propriament ellas se appellan figuras de las quals las 9 se appellan figuras significativas. et la 10 se appella chifra o figura de non res car non val res mas que fa valer las autras segont lo loc en que es.

Per so es neccessari que n'i aja una que non valha res per raso de las 10 entieras las quals non se poden scriure sens aquella.

Et fan se las figuras en aquesta forma 0/9/8/7/6/5 4/3/2/1. De las quals la premiera que acomensa a la part dreyta val un. La seconda 2 La tersa 3 e la quarta 4 e aixi metes las autras entro a la desena que non val res. mas que fa valer las autras. 1/2/3/4/5/6/7/8/9/0

Item deves saber que per contar non son mas tres nombres generals que se appellan simple nombre, desena et centenal.

Simple es la valor de las figuras e totz temps es en lo premier loc del ternari de la part dreyta car en aquell loc non valen simplament si non lur valor o significatio de desena que es tot non que se pot metre en 10 partidas engoals de dintre 100 o que non val res car es chifra e totz temps

es en lo segont loc del ternari e son como dirian /10/20/30/. E aixi dels autres.

Centenal es lo nombre que se pot pausar en 10 partidas egoals entro a 9 partidas o non res si es chifra. Et totz temps es en lo tertz loc del ternari en vers la man dreyta o en lo premier davers la man esquerra.

Et ayxi aprop que cascuna de las figuras d'aquels tres nombres pot accuppar lo loc com fa la chifra que non val res mas que accuppa lo loc per la qual accupatio hom li atribuisson aquels tres nombres general, non remens que premierament parlam que ella non aja ges per son nom res significar.

Item per contar es mais de saber que aquetz tres nombres generals alcunas vegadas son sens denguna denominatio com es en lo premier ternari so es en las tres premieras figuras que son davers la part dreyta. E en totz los autres ternaris sien complitz o non els an denominatio. E per so es que cascun ternari sie complit o non que lo procesis vers la part esquerra lo tertz de una denominatio. Car lo segont ne ha una, lo tertz 2 lo quart 3 e aixi seguentment. E aixi aprop que dit es sien los tres nombres.

si son complitz o non en lo segont ternari deven dire milhier. E en lo tertz mil milhie et en lo quart mil mil milie. E aixi dels autres segont que requier lo nombre dels ternaris.

E per so appar que nul propriament non es pas nombre mas es denominatio dels autres nombres desus ditz.

A contar doncas una granda suma ho un grant nombre premierament hom deu devesir las figuras de tres en tres segont los tres nombres acomensant las de devesir davers la part dreyta. E aprop hom pot scriure qui val lo nombre de las denominatios aixi com aissi appar 324( 5 ) 043( 4 ) 503( 3 ) 140( 2 ) 453( 1 ) 343( 0 )

Item deves saber que per lo contar que dues denominations ensemps que son miell milie vulgarment se expremissen per aquest vocable milio. Car un milio es miell millie.

E per so qui ha explicar un grant nombre deu regardar si lo nombre que denota las denominations es par ho non par. E si ell es par per cada vegada que hom hi troba 2 devem dire milions com si eran 4 hom deu dire milions de milhiers. E si era 6 hom deu dire milhiens milies de milhiens. E senblament dels autres

pars. E si ell era en nom par per lo 1 solet premierament hom deu dire miell e aprop per cada vegada que hom hi atrobara 2 hom deu dire milhens com si era 3 diriam mille millions millie per la 1 solet. E millions per los 2. E aixi aprop que totz los nombres montan e se governan per lo [no]mbre de 10.

[2] Com deves ajustar.

Ajustar es diverses nombres metre en un lo qual solet valha tant com totz los autres ajustatz e non mais ni mentz. E aysso per explicar los totz per una suma per la qual causa saber fer. Lo son 3 reglas per las quals entendre ho devem.

E deves saber que lo son 3 nombres que se appellan simpla desena. Et mais que desenas son las valors de las 10 figuras com es dit al capitol desus, desena son los nombres que se poden metre en 10 partidas egoals entro a 9 partidas. E son 9 desenas que se denominan per las 9 figuras significativas. Como 10 per 1 e 2 per 20 et 3 per 30 et 4 per 40 E aixi entro a 90 que es la derriera figura. Plus que desena es tot nombre que ha desena entieyra es plus una de las 9 figuras significativas qual que sie como 11, 12, etc

21, 22, etc 31, 32, etc 41, 42, etc 51, 52, etc 61, 62, etc 71, 72, etc 81, 82, etc 91, 92, etc. E aixi meteis de totz los nombres contengus en 3 desenas entieras propdanas com 20, 30, ho 40. E senblament de las autras.

Item segondament per pausar las reglas seguens en practica deves saber que totas las figuras de un orde se devem escriure en tal maniera que totas sien la una dreyt del autra desus ho dejos como totas las premieras acomensant a la part dreyta sian dejos la premiera desus. E totas las segondas dejos la segonda. E las tersas dejos la tersa e aixi de las autras continuant vers la part esquerra la qual maniera de escriure servada hom deu ajustar segont la practica que dona la regla de 3 que son tres seguentz de las quals la premiera regla es aquesta seguent.

[La premiera regla]

Si per l'ajustar, de totas las figuras de un orde lo ne ve nombre simple qualque sie aquell, de las figuras hom deu escriure la figura representant aquell simple en dreyt d'aquell orde.

La 2 regla.

Si per l'ajustar, de totas las figuras de un orde lo ne ve desena, hom deu escriure chifra de dreyt d'aquell orde et servar la

figura de la desena venguda la qual se deu scriure e contar ab lo plus propda orde que s'en siec o se deu escriure per si si non s'en siec res en tal maniera que ella fassa un orde.

La tersa regla.

Si per lo ajustar de totas las figuras de un orde lo ne ve plus que desena hom deu escriure lo plus de dreyt aquell orde e far de la figura de la desena com es dit en la regla precedent.

	7	0	8	3	0
	6	0	7	3	0
	3	0	5	2	0
1	6	2	0	8	0

Eyxemple

Per declaratio veses que tot lo premier orde son 0 que es simple per que escriu la figura denotant aquell simple perque escriu la figura denotant aquell simple que es 0 per la maniera de la regla.

Item lo segont orde so es 33. e 2 son 8 [que es simple per la premiera regla escriu] 8 dejos lo segont orde.

Item ajusta lo tertz orde so es [875] montan 20 que es desena per so escriu 0 per la segonda regla dejos lo tertz orde e garda 2 que es la figura de 20 Item ajusta lo quart orde que es tot 0 per que es 0 et 2 que tenes que li deves ajustar per la segonda regla monta 2 perque escriu 2 per la premiera regla dejos lo quart orde.

Item ajusta lo cinque orde so es 763. monta 16 que es plus que desena per so escriu lo plus per la tersa regla dejos lo cinque.

orde que es 6 e garda 1 que es la figura de una desena. E car non s'en siec res escriu lo detras 6 que fasan un orde como ditz la segonda regla e sera feyt aquell ajustament. E aixi fey de totz los autres nombres la qual causa entendas de mais o de mentz segont la multitut de las summas.

Car aquellas 3 reglas supplissen a totz los entiers de una meteyssa valor ni plus se extenden si non a las causas desemblans.

Regla per ajustar causas desemblans.

Et si vols ajustar nombres rotz los quals se meten per maniera de entiers segont diversas valors com per eyxemple qui voldria ajustar bell colp de summas que en cada una agues liuras, soutz et deniers e aixi de las autras causas senblans et non remens aven orde en lur valor per so que las mendres son partidas de las majors et es una regla que es tala sequit regla.

Quant aures ajustadis totas las summas segont las reglas desus ditas de la causa de mendre valor, leva ne d'aquella summa totz los entiers que tu poyras de la causa que se siec propdanament que val mais los quals entiers ajusta ab aquella causa que mais

val aqui es senblant. E si resta res que non puesca venir a un entier, escriu ho en aquell orde que tu as ajustat.

Et senblantment fay aprop de las autras summas mejancieras entro pertant que vengas a la causa que es de major valor en la qual tant solament se servan las 3 reglas premieras.

Como per eixemple qui deuria ajustar liura, sou et denier. Premierament de ajustar los deniers e si en aquella summa de deniers se atroban souses entiers hom los deu ajustar ab los souses et los deniers que restarien dejos los deniers aprop ho deu hom ajustar totz los .souses. ab aquells .deniers. et quant son ajustatz hom deu gardar quantas liuras valen la quals se deven aprop ajustar ab las liuras seguentz si n'i a e los souses que restan se deven escriure en lo loc dels souses com los deniers. E aixi se fa lo ajustar de causas senblans.

Lo tertz capitol que ensenha de sostraire.

E sapias que sostrayre es lo contrari de ajustar.

Sostraire es levar un nombre de un autre que li sie egoal o major per saber de quant sera major.

Premierament es de saber que en lo sostrayre no a mas 2 nombres principals, so es lo nombre que se deu sostrayre e lo nombre

del qual se deu sustraire los quals se deven escriure figura per figura com es istat dit en l'ajustar e del major del qual se fay la sustratio ne falh lo tertz que se apella lo sobreplus. Lo qual se deu escriure dejos de dreyt figura per figura. Aixi com a l'ajustar.

E deves saber que hom cognois lo major nombre en dues manieras. La premiera es quant ha mais de figuras com es aquest eyssemple en lo qual nombre lo dessus es major que lo dejos per so car

1	0	0	0	0
	9	9	9	9

hi a 5 ordes. Et en lo dejos non n'a que 4. Item manuscrich: segondamament segondament se cognois la major quant ha tantas figuras en la un como en l'autre. A la premiera que mais val acomensant a la part esquerra como appar en aquest eixemple. En

3	4	5	7
3	4	6	0

lo qual nombre lo dejos val mais que lo desus per rason del 6 que val mais que lo 5 que es desus.

Per saber doncas sostrayre lo menor nombre del major pueys que ells seran servitz per lurs figuras com es istat dit lo son 4 reglas generals per las causas senblans de las quals la premiera es aquesta

Si tu levas una figura de sa senblant scriu 0 desus ho dejos de dreyt aquella figura de la qual tu as levat sa senblant. Si tu levas una figura de una autra major scriu aquo de que es major de dreyt com es dit en la regla desus.

E si tu deve levar una figura de una autra mendre, mendre car lo no se pot fer, manleva 1 de la plus propdana figura significativa d'aquella summa de la qual tu fas la sustratio lo qual 1 conta? per 10 e pueis d'aquella desena ab la figura mendre ajustada si es figura significativa tu leva la major que tu volias sustrayre e so que restara de dreyt scriu lo loc del qual s'es feyta la sustratio com es istat dit en la premiera regla.

Et si hi a 0 ho 00 mejanciera entre lo loc que tu as pres lo 1. E lo loc en que l'as contat per 10 la cascuna 0 conta per 9 ho ne fey figura de 9 dels quals 9 tu fay ta sustratio si hi a figura a sustrayre. Eyxemple leva 7 de 2 non pot falhir, manleva 1 per la tersa

4	0	2
3	5	7
0	4	5

regla dels 4 et restan n'i 3 aquell 1 val 10 e 2 que n'i a e son 12 de que leva ne 7 restan 5 Item leva 5 de la 0 val 9 per la quarta regla et restan 4 per ? regla.

Item

leva 5 del 0 que valen 9 per que hom ne aura manlevat 1 resta 0 per la premiera regla.

Et aixi sustrayre $\frac{35}{7}$ de 402 restan 45. E aixi aquest eyxemple de 3 figuras manuscrich: paratica suplis e demostra la pratica de las 4 reglas e las 4 reglas suplissenapropera a sustrayre en totas causas.

Et si hom volia sustrayre nombres rotz los qual se pausan per maniera de entiers com es dit desus en lo ajustar, non remens que ells sien diverses els an orde en lur valor car los uns son partidas dels autres com es de las liuras et dels souses et dels deniers perque per sostrayre los mendres dels majors ne dona tala regla.

Servant las 4 reglas sobremesas en cada orde si es neccessari de manlevar de autre orde de valor [?] manleva 1 lo qual conta per tant quant val 1 del plus propdan orde delqual se deu fer la sustratio. E de aquella valor de un que tu has manlevat ab aquo que hi era davant tot ajustat fey ta sostractio. E lo sobreplus escriu de dreit aquell orde.

Et si hi avia orde o ordes de valor mejanciera en que non ? res en lo cascu layssa o scriu lo major nombre que se deu escriure segont la valor d'aquel

orde dels quals nombres layssantz tu continua la sustractio segont que requeriran las summas que te deven sustrayre.
Eyxemple general per totas causas.

Qui deurie sustraire liuras, souses, deniers e era neccessari de manlevar souses per sostrayre los deniers aquell souses se deu contar per sa valor que ell ha en conparansa dels deniers que ne valen 12 dels quals 12 deniers ab los autres si ni avia tot ajustat fey ta sustractio dels deniers Et quant tu vendrás a sustrayre lo sou e has mestier de manlevar 1 liura. tu la deves contar per 20 souses. que val dels quals ab los autres ajustatz lo se fey la sustractio dels souses

Item qui deurie sustraire liuras souses et deniers et pageses e fa sie mestier de manlevar per eyxemple 1 liura per sostrayre las pagesas d'aquella liura se deu contar per 1 denier que val 4 pagesas que es la valor del orde plus propda de las pagesas et d'aquell denier fer la sustractio de las pagesas.

Et quant es feyt en lo orde dels souses hom deu escriure 19 que es lo major nombre que se deia escriure en aquell orde. Et en lo orde dels deniers hom deu escriure 11 que es lo derrier nombre que se deu escriure.

Et aprop si es necessari de sustraire deniers ni souses ells se

deven levar d'aquells que an escriutz aprop que an manleut de la totalitat. Et aixi aprop la maniera de sustrayre en causas semblantz et desemblans non remens en lur valor.

Et qui voldra proar si ha ben
feyt ajuste lo nombre que ha sustreit ab lo sobreplus de la major de la quala ha feit la sustractio e trobara la major si ha ben feyt.

Per autra maniera de parlar ajusta las dues mendres summas. Car si la sustractio es ben feyta hom atrobara la major summa autramens non.

Senblanment qui voldra provar lo ajustat quant aura ajustat 2 summas sustrara 1 de las summas ajustadas de la summa de tot. Car sustraent la una per la sustraction trobara l'autra si ha ben feyt autrament non. Et aixi aprop que l’ajustar prova lo sustrayre. Et lo sostrayre prova lo ajustar per raso de aquella regla general un contrari prova l'autre.

Lo tertz capitol que ensenha de multiplicar es per aver la practica de multiplicar. Convenient es de entendre premierament que vol

dire multiplicar.

Multiplicar es un nombre atrobar, en lo qual entierament es contengut lo cascun dels nombres que se multiplican (tantas vegadas) como ha de unitatz en son contrari. Per declaratio d'aquesta descriptio deves saber que en la multiplicatio non ha mas 2 nombres los quals se deven escriure figura per figura como es dit en lo capitol del ajustar dels quals la un se appella multiplicant et l'autre es aquell que es per multiplicar, los quals 2 nombres son contraris.

Et tot temps lo menor de els sera multiplicant entendent per lo mendre nombre quant per tot lo nombre.

Car qui fasie lo contrari lo vendría tot ad un nombre lo qual se atroba per la multiplication d'aquels 2 nombres contraris lo qual se appella summa de tota la multiplicatio. La qual summa conte tantas vegadas lo cascun dels como ha de unitatz en l'autre. Per la qual summa profitament saber la taula seguent la qual taula se appella lo petit libret. En lo qual se conte la multiplication de totas las 12 (?) figuras de la cascuna en si meteyssa. Et en totas las autras lo qual libret se fey en tal maniera per abreviar la multiplicatio. La quala es la plus breva que se puesca fer.

		1 1	2 2	3 3	4 4	5 5	6 6	7 7	8 8	9 9	0 0
		4 2	6 3	8 4	10 5	12 6	14 7	16 8	18 9	0 0
		9 3	12 4	15 5	18 6	21 7	24 8	27 9	0 0
		16 4	20 5	24 6	27 7	32 8	36 9	0 0
		25 5	30 6	35 7	40 5	45 9	0 0
		36 6	42 7	48 8	54 9	0 0
		49 7	56 8	63 9	0 0
		64 8	72 9	0 0
		81 9	0 0
		0 0

Per declaratio d'aquest
libret deves saber que la premiera figura de cascu orde multiplica si meteyssa e totas aquellas que se seguissen en aquell orde. En las quals en aquellas desus que son de tinta negra es la summa de las multiplications

que las voldra atrobar per art ab la pluma o de cap yeu ne doni 2 talas practicas. La premiera de la mendre figura fen ne 10 E aprop multiplica aquella meteyssa figura menor per los nombres de las unitas que son de la major entro a 10 feyta de la menor figura e so que restara es la summa que tu voles Exemple multiplica 7 per 6 e fey 10 del 6 monta 60 aras de 7 entro a 10 ha 3 per so digas 3 vegadas 6 son 18 leva 18 de 60 restan 42 Et aixi faras de totas las autras.

Semblanment si una figura multiplica si meteyssa que ne fas fas [sic] major o menor. Exemple multiplica 8 per 8 fan 80 aprop de 8 entro a 10 ha 2 digas 2 vegadas 8 fan 16 sustray 16 de 80 remanen 64

Autra practica per la ? partida multiplica la mendre figura per las unitatz que son de la major entro a la 10 la 10 enclusent. E aprop garda de quantas desenas conte aquella multiplicatio sien complidas ho no. E per cada 10 que contendra leva ne 1 de mendre figura e davant aquo que restara met lo nombre de las unitatz que restaran a complir la 10 de la multiplicatio ho 10 si la multiplicatio era istada 10 entiera. Exemple multiplica

8 per 6 de 8 entro a 10 ha 2 per so digas 2 vegadas 6 son 12 et 12 es de 210.^nas per so leva 2 de 6 restan 4 aprop de 2 entro a 20 que es la 10 seguent la multiplicatio lo hi a 8 que deves metre davant 4 e son 48 ?ien multiplica 8 per 5 de 8 entro a 10 ha 2 digas 2 vegadas 5 son 10 que es de una 10 E per so leva 1 de 5 restan 4 E car la multiplicatio es istada 10^na entiera met 0 davant los 4 e fan 40

E aixi fey de las autras e senblament si 1 figura multiplica si meteyssa que ne fassas major e menor.

Aysso es la practica de multiplicar 1 figura contra 1 figura.

Aras resta la practica de multiplicar diversas figuras aprop 1 figura o diversas figuras per diversas figuras. Et per so deves saber que las reglas del ajustar servissen a escriure las multiplications. E aprop alevar la summa per que enclusent las 1^a regla es aquesta.

Oservant las reglas del ajustar la 10 escriu en la seguent multiplicatio lo simple de la premiera de dreyt escrivent de la multiplicant.

Per declaratio d'aquesta regla deves saber que ella a 3 partidas. La 1^a es que hom deu servar totas las reglas.

del ajustar en la maniera de l'escriure. La 2a es que quant per la multiplicatio de una figura contra l'autra ne ve 10a que hom deu gardar aquella 10a entro atant que hom aja multiplicat 1^a autra figura si tant es que ni aja a multiplicar e la vegada hom deu ajustar aquella desena ab aquella multiplicatio ho escriure la per si que tenga orde si non hi a plus figuras a multiplicar.

La 3 partida de la regla es que lo simple de la premiera multiplicatio se deu escriure dreit de la multiplicant per tal declaratio et senblantment de la 2a partida es de saber que cada figura del nombre multiplicat deu multiplicar totas las figuras del nombre que se deu multiplicar per que aprop que la una figura del nombre multiplicant acomensat de multiplicar las figuras del nombre que se deu multiplicar. Ella non deu cessar entro atant que ella aja multiplicat totas las figuras de son contrari. Empero so es que la premiera multiplicatio se appella a cascuna vegada que las figuras del nombre multiplicat la premiera que es a la man dreyta del nombre que se

deu multiplicar. E la vegada hom deu acomensar de escriure de dreyt a la multiplicant. E aixi que hom la continue de multiplicar, las autras figuras seguens hom deu continuar de escriure ves la ma esquerra figuras per figuras ab degutz ordes per tal que quant vendra a levar la summa de la multiplicatio que las figuras non sien enpachadas. E per major declaratio pausarey 1 exemple de 3 figuras conta autras 3 figuras per lo qual exemple se entendan de fer totas las multiplications sien de mais ho de mentz per la qual yeu voli multiplicar 345 per 273

		2	7	3
		3	4	5
	1	0	3	5
2	4	1	5
6	9	0
9	4	1	8	5

x que? declaratio del exemple veses que los 3 multipliquan los 5 e fan 15, scrives 5 e tenes 1; aprop multiplicas los 4 e fan 12 e 1 e son 13, escrives 3 et tenes 1. E aprop multiplica los 3 e fan 9 e 1 son 10 scrives 0 aprop 1 per solet car non hi a autras figuras a multiplicar

Item los 7 acomensan de multiplicar los 5 que fan 35 e acomensas de scriure 5 dejos los 7 tot dreyt e gardas 3; aprop multiplica

los 4 [*] aisso que [*] fan 28 et 3 e son 31, scrives 1 & gardas 3; aprop multiplicas 3 e son 21 & 3 & son 24, & escrives 4. Et car no hi a autra figura a multiplicar scrives 2 detras los 4 fassan 1 orde.

Item los 2 comensant de multiplicar los 5 e montan 10, scrives 0 dreyt dels 2. E gardas 1; aprop multiplica los 4 e fan 8 & 1 e son 9, scrives 9 detras la 0 aprop multiplicas los 3 e fan 6 que escriures detras los 9 dejos los 2. Et aixi apropera com las figuras seran scriutas figuras per figuras a degutz ordes.

Aras levas la summa e premierament scrives 5 detras lo 5 aprop ajustatz lo 2 orde et digas 3 e 5 son 8 scrives 8 detras lo 5 Et aprop ajustatetz lo 3 orde e digas 0 e 1 et 0 es 1 escrives detras los 8. Aprop ajustatz lo 4 orde e digas 1 e 4 e 9 son 14 scrives 4 detras lo 1** et tenes 1 que deves ajustar ab lo 5 orde. E dire 1 et 6 et 2 son 9 que deves scriure detras lo 4 E aissi se fa la summa de la multiplicatio monta tot 94185 Et aixi appar la practica del multiplicar una figura per una figura o diversas figuras per una figura o diversas figuras per diversas figuras.

Autra practica per multiplicar

La practica autra per multiplicar es car per desmembransa de retenir o de ajustar las 10as de las multiplications precedens ab las multiplications seguens, hom es bell colp de vegadas enpachat et las multiplications ne son falsas.

Per so

per multiplicar plus segurament e ab mens de pena. Et per fer una granda multiplicatio en mendre plassa. et que no hi sie necessaria de retenir las desenas o mas de tot pausar a cascuna vegada que multiplicarem 1 figura per autra. Yeu pausi aissi 1 autra practica comuna et leugiera la qual es aquesta seguent. Premierament hom deu escriure 1^a de las 2 summas que voles multiplicar per sas figuras, aquella que hom se voldra, sie la major o la menor en summa o en nombre de figuras.

Aprop hom deu fer figura cayrada dejos aquella summa en la qual figura hom deu fer dejos cascuna figura tantz cayratz com hi a de figuras en la summa que deu multiplicar . La qual autra summa se deu escriure a la un costat de la figura cayrada en aquell que hom se voldra sie a la man dreyta o a l’esquerra. Et aisso en tal manieyra que la figura denotant lo major nombre d'aquella summa que serie la premiera daves la part esquerra si se escrivia de dreyt sia d'aquest sobiran cayrat d'aquell costat. Et las autras figuras sien segont los ordes en devallant la cascuna acosta son cayrat. Aprop deu hom partir cascun cayrat per lo mieg fasent 1^a linea que tire del angle desus daves la part dreyta al

angle contrari que es dejos daves la part esquerra la qual causa feyta hom deu fer la multiplicatio en tal maniera que cascuna figura del costat multiplisse totas aquellas desus acomensant ad aquella que vos voldres mas que hom escriva la multiplicatio de dintz lo cayrat que es de dreyt la cascuna figura de las 2 que se multipliquen tostemps escrivent. La desena en la mittat desus del cayrat et en l’autra mittat dejos lo simple. Et quant la multiplicatio sera complida hom deu ajustar las figuras que son entre las linias que parten los cayratz en 2 partidas acomensant a l’angle dejos daves la part dreyta. Car la figura que es la mittat dejos d'aquell cayrat fey lo premier simple de la summa de tota la multiplicatio. Et la figura que es en l’angle contrari que es desus daves la part esquerra es la figura derrieyra denotant la major summa de tota la multiplicatio que tostemps es premiera daves la part esquerra.

Et per tal que hom vera miells aquesta pratica yeu pausarey alcuns eyssemples en los quals pertant que hom hi vera miells las quals figuras hom deven

ajustar totz los cayratz partitz per lo mieg ab vermellio. Et aixi ho deu hom ajustar las figuras que seran entre las lineas vermellias acomensant al angle dejos com es dit.

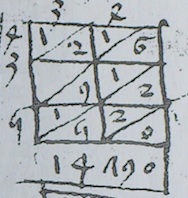
Per declaratio d'aquestas figuras que per eyssemples podes veser que per levar la summa en las 2 premieras hom escriu premierament 5 aprop las 3 figuras seguens que son 835 aprop las autras seguens que son 12210 E aissi procedent ves la part esquerra. E en las autras acomensant en la 0 aprop las 3 seguentz 225 E en aquesta maniera se fassa si hi avia mais o mentz de figuras. Et qui pausara las figuras del costat per lo contrari so es que la major summa fossa dejos hom partira los cayratz per lo contrari so es que la major summa fossa dejos hom partiria los cayratz per lo contrari et las 1O^as. se escriurien dejos. Et las simplas en la mittat desus aprop hom acomensariam

a levar la summa al cayrat desus de la par dreyta continuant vers la part esquerra que es contrari del pausar e del levar desus. Et aysso abaste per aquesta practica.

Que es progressio: progressio se ajusta per la multiplicatio

E  deves saber que alcuns nombres en certa maniera ordenas son manuscrich: perftament plus perfieitament ajustatz per la multiplicatio que non son per lur capitol del ajustar. Et la maniera de ordenar aquells nombres se appella progressio de la qual alcuns fan capitol expres. Non remens que ab honor parlant segont la practica ell non serie punt capitol mas alcuna presta manieyra e practica de ajustar aquells nombres la qual practica se prova per lo capitol de ajustar per manifestar que vertat es lo ajustar de la multiplicatio.

Et si voliam dire que lo sie capitol per rason de hutilitat de las reglas. Car las 2 premieras que ells pausan valen ad atrobar los nombres triangulars.

La 3 per atrobar los nombres quadriangulars. Et la 4 per atrobar los nombres cayratz entiers. Et aquella rason non ha ayssi loc. Car aixi s'en tracta per la practica de prestament ajustar aquels nombres et non pas per aquella rason.

Item que si disiam que per la parcialita

de la practica la rason non es suffisent car autres nombres hi a que per practica special del multiplicar lo se poden ajustar com yeu lo demostrarey del quals senblantment ne farey capitol special mas car tot se fa per la multiplicatio yeu ho conprendi en lo capitol del multiplicar.

Et non rementz mas que yeu aja dit que vol dire progressio e la aja devisida en sas partidas yeu ne darey 2 reglas sufficientz ad ajustar totas progressions. Per so vejam que vol dire progressio.

Et sapias que progression es una ordenansa de nombres tal constituit per ajustament de 1 nombre determinat, en lo qual lo segont sobremonta lo precedent. Como per eyssemple Pausi 3 nombres so es 345 denotant como lo segont, que es 4 sobremonta lo 3 de tant sobremonta lo terz, que es 5 lo segont que es 4 Et aixi se deu entendre si n'i avia diverses e de tota autra progressio. Car yeu hey dit que la devisiria.

Et deves saber que la progressio ha 3 specias, so es lo son 3 progressions. La premiera se appella natural. La 2 se apella no natural ho progressio rota. La 3 se apella en partida non natural. Et en partida natural es aquella que acomensa a 1 et continua per lo ajustament de 1 Como 1, 2, 3, 4. et

les quals segueyssen sobremontan lo precedent tant solament de 1. Lo [non] natural es aquell que se acomensa a 1 [et] lo nombre que se ajusta es autre nombre que 1 o que non acomensa ad 1 ni lo nombre que si ajusta non es 1. Et aixi aprop que la non natural pot acomensar en tot nombre e pot ajustar tot nombre si non 1 Aquella que es en partida natural e en partida non natural es aquella que non acomensa ad 1 e lo nombre que si ajusta es 1 Per so ella pot acomensar en tot nombre si non ad 1 et non pot ajustar autre nombre si non 1 E appella se en partida natural car continua per ajustament de 1 aixi com la natural. Et se appella en partida non natural mannescrich: comensa car non ha comensat en 1 com fa la natural.

E aixi appareys que vol dire progressio e cals son sas partidas, per que per saber ajustar.

Et tals nombres son las reglas seguens.

La premiera regla

Si lo nombre dels loncx es nombre en non par, multiplicant tot lo nombre dels loncx per nombre occupant lo loc mejancier e auras la summa de tota la progressio. Eyxemple : pausa 3 nombres 357 multiplica 3 que es lo nombre dels lonx per 5 que ocupa lo mieg, monta 15 Et a tant

montan.

Et aixi deves fer de totas progressions dels nombres dels loncx que son en non pars.

La seconda

Si lo nombre dels loncx es par, ajusta lo premier ab lo derrier de la qual summa multiplica per la mittat del nombre dels loncx, e auras la summa de la progressio. Eyxemple pausa 4 nombres 2468. ajusta 2 ab 8 son 10 que deves multiplicar per 2 que es la mittat dels loncx monta 20 et aixi fay en totas las progressions en las qualas lo nombre dels loncx es par. [Et entendas per las reglas que cascun nombre per petit o per grant que sie ell fey ? lonc[

Per ajustar los nombres que venon per continua duplatio et aysso per continua multiplicatio.

Et deves saber que autres nombres son com yeu hey dit desus en autra maniera ordenatz que non son aquels de la progressio son plus prestament ajustatz per la multiplicatio que non son per l'ajustar los quals nombres se ordenan per continua duplatio como son 124816 Et aixi continuant tant quant hom voldra, et mais que acomensen ad 1 aytals nombres an tal proprietat que lo derrier monta mins 1 de totz los autres, perque qui voldra ajustar las duplations que aurie feytas doble lo derrier, e leve ne 1 e aura la summa que vol. Eyxemple yeu voli ajustar

5 nombres ordenatz per aquella maniera que son 124816, dobla 16 son 32 leva ne 1 restan 31 E aquo es la summa d'aquels 5 nombres. Et semblament se deu entendre de tot autre nombre que es per continua duplatio. En qualque nombre que hom comense qui dobla lo derrier, aprop ne leva lo premier, ell ha la summa de totz aquels nombres. E aixi termina la practica del multiplicar.

Aprop que yeu hey dit de la practica del multiplicar convenient es que yeu done la cognoyssensa de son contrari que es partir la qual partir generalment es metre una summa en 2 o diversas partidas segont las proporcions en las quals era prepausat de metre la summa mesa a partir. Per major declaratio de la diffinicio mesa et de tot lo capitol es de saber que lo partir ha 2 especias; so es que ell conten 2 manieras de partir. La una ensenha de partir una summa en partidas engoals segont que rederen las proporcions prepausadas a fer lo partiment, de la qual vol tractar per reglas et per eyxemples en la 3 partida generals d'aquest compensi en la qual darey doctrina de fer las rasons como ey prometut al comensament en la division d'aquest compendi.

L'autra maniera de partir ensenha de partir una summa en partidas engoals, delqual entendi de parllar en aquest capitol car ella es plus general que l'autra. Car l'autra non se pot fer mens la practica d'aquesta.

Per so yeu ne doni 2 aytals diffinitions. Partir es cercar un nombre lo qual es contengut entierament tantas vegadas en lo nombre que se partis com ha de unitatz en lo nombre que es partidor.

Et la segonda diffinicio es per partir un nombre que demostre quantas vegadas lo nombre partidor entierament es contengut en lo nombre que se partis.

Et per cognoyssensa major d'aquestas diffinicions es que cada partiment servis a 2 causas. La premiera es per partir una summa a diverses en lo qual partiment atroba hom lo dreyt de un solet per lo qual sabem que deu aver cadaun o cascun car son engoals. Et en aquest prepaus es la premiera diffinitio.

La 2 diffinicio o causa que fa lo partiment es que met ho retorna la summa que es de causa de mendre valor en la sua sobirana como per eyxemple qui valdria retornar deniers en souses et souses en liuras. Et en aquest prepaus es la 2 diffinicio per las quals es mais de saber que en lo partir ha 3 nombres: so es la summa quee lo partidor

e lo nombre que se atroba per lo partir que se appella nombre denotant que ve per lo partiment, lo qual se deu escriure entre 2 lineas feytas en aquesta maniera: que la summa que se partis sie desus et lo partidor sie dejos lo qual es totz temps 1 entier.

Aprop que yeu hey dit que vol dire partir, generalment et particularment de la partida de la qual especialment es lo present capitol disent a que aprofieyta e la maniera de l'escriure.

Resta que yeu pausi la practica per la qual es de saber que alcunas vegadas hom partis per una sola figura signifficativa.

Et alcunas vegadas per 1^a sola figura signifficativa alcunas per 2 o per diversas segont que requier lo partidor. E car normalment nos procesissem en tot quant fasem et aprenem a comensar a las causas plus defficils.

Per so premierament darem la practica de partir per 1 figura milhor que per 2 ni per tropas per partir doncas per una figura aquesta es la regla.

Aprop que la summa que se deu partir es scriuta per sas figuras et las 2 lineas son feytas, et la figura que deu partir es escriuta dejos

figura per figura segont l'orde dejos lo qual deu esser per rason hom deu regardar quantas vegadas es contenguda entierament la figura queen la premiera figura de la summa que se deu partir, e lo nombre de las vegadas que es contenguda escriure dejos entre las 2 lineas et si restava res de la figura lo se deu escriure desus et cancellar la premiera. Senblantment se deu fer de la 2da si non restava res de la premiera & si era res restat hom ho deu contar per 10 en la 2 figura. Et la vegada hom deu gardar quantas vegadas es contenguda entierament la figura que partis en aquella 10, e segonda figura ensemps, e lo nombre de las vegadas se deven escriure dejos la 2 figura et si resta res desus se deu escriure com es istat dit de la premiera figura. Et per aquesta maniera se deu continuar entro que hom ajan escriut lo nombre de las vegadas dejos lo orde dejos lo deu restar la figura que partis per rason avisant se que non reste degun orde detras lo orde del partidor que non hi aja escriut qualques figura per tal que las autras non perdan lur

valor.

Per declaratio d'aquesta regla es de notar que quant la figura que se deu partir es mendre que lo partidor e non hi aja 10nas que hom deu pausar 0 dejos e resta aquella figura entiera la qual se conta aprop per desena, si es figura significativa en lo segont partiment, si tant es que si ensiega.

Per eyxemple, voli partir 8123 per 3, aras digas en 8, quantas vegadas es 3, ell si atroba 2*, * per so escriuz dejos los 8 restan autres 2 que deves pausar sobre los 8. Item per rason dels 2 que son restatz, digas en 21 quantas vegadas sal 3, ell si atroba 7 vegadas, per so scriu 7 dejos la 1 et resta non res per que cancella los 2 et lo 1 Item digas en 2 quantas vegadas sal 3, non deguna car 2 es mendre que 3 et non resta res detras, per que escriu 0 dejos manca: 8123÷3=2707 restan 2, doncas deuria ajónher: en 23 quantas vegadas sal 3, si atròba 7 e réstan 2. los 2, et es feyt car resta orde per orde & so que resta es mendre que lo partidor et aysso es la manieyra de partir per una figura.

Aprop que yeu ey donat la pratica de partir per 1na figura resta que yeu done la practica de partir per 2 o per tropas figuras per la qual practica aquesta es la regla general.

Aprop que la summa que se deu scriure es

scriuta per sas figuras et las 2 lineas son feytas hom deu metre la premiera figura del partidor dejos la premiera que se deu partir & la 2^a dejos la 2^a & ayxi de las autra[s] si mais ni avia continuant vers la part dreyta. Aprop hom deu regardar quantas vegadas se pot levar la premiera figura del partidor de la premiera figura de la summa que se deu partir, e aysso en tal maniera que tantas vegadas ne poscan falhir las autras seguentz ab so que resta de la premiera si resta res & si de la premiera non restava res o so que resta en las autras figuras desus non suplis per fer la substractio hom deu deyssendre lo nombre quociens de la premiera entro a tant que so que restara supplisca. Aprop que hom ha vist quantas vegadas se pot levar e que las autras desus per ellas ho an so que restara subpliscan a la substractio de las autras lo nombre de quosciens se deu desus la derriera figura del partidor. Et aprop per aquell nombre fer la substractio de las autras figuras del partidor. Et aixi en lo nombre que es desus lo partidor non deu res restar & si resta res deu esser mendre que lo partidor. Item mais que quant aquell partiment

es feyt hom deu mudar lo partidor e metre la premiera figura del partidor dejos la segonda d'aquell que se deu partir, e la 2^a del partidor dejos la 3^a senblantment de las autras continuant vers la part dreyta. Et quant lo partidor sera mudat hom deu avisar si hi era res romas de la premiera ho non, et si non es res romas hom deu fer la 2^a com es istat dit de la premiera. Et si era romas alcuna causa de la premiera hom lo deu contar per 10^a en la figura e ajustar tantas vegadas es contenguda la premiera del partidor que es dejos la 2^a de la summa que se deu partir en aquella 10^a, et la 2^a figura ho so que es restat en lo loc de la 2^a ensemps en tal maniera que las autras del partidor se puescan tantas vegadas substrayre de las desus ab so que resta si resta res, e si non supplis que devalle lo nombre quociens de la premiera entro atant que so que restara supplisca a la substractio de las autras. Et lo nombre quociens se deu escriure sobre la premiera del partidor en maniera que lo nombre que es desus lo partidor resta mendre que lo partidor ho non res.

Et en aquesta maniera

se continua la mutatio del partidor entro a tant que ell sie en son loc figura per figura, continuant la substractio de las autras figuras & lo escriure de las figuras denotant quantas vegadas en tal guisa que non hi aja dengun orde dejos la qual non aja qualque causa escriut de la premiera fins al loc de la premiera del partidor . Et aixi deu en devenir que en lo nombre que se partis non deu res romandre & si resta res deu remandre mendre que lo partidor.

Per declaration de la regla & per aver la practica plus presta lo son 5 causas de notar. La 1^a. que quant lo es dit en la regla que la 1^a del partidor se deu levar tantas vegadas quant hom pot de la premiera de la summa que se deu partir. Que per la premiera es entendut la premiera daves la part esquerra que representa lo major nombre en la cascuna summa so es lo partidor et en la summa que se deu partir.

Item 2^ment que de dintz las 2 lineas feytas dejos la summa non se deu res escriure si no lo nombre que representa quantas vegadas hom pren la premiera del partidor de la summa que li es desus en la qual summa non se pot plus pendre de 9 vegades [sic]

ni mentz de 1^a vegade [sic].

Item 3^ment es de saber que figura per figura semblament quant se conta per 10^as, es 9 vegadas, resta tant quant val la figura. Per eyxemple en 40 quantas vegadas es 4. Ell hi es 9, & restan 4.

Item en 50 quantas vegades es 5. Ell hi es 9, & restan 5. Et aixi dels autres.

Item 4^ment quant la figura de la qual se deu levar la 1^a del partidor sera mendre que la premiera del partidor et non ha 10^a detras hom deu scriure 0 dejos aquella figura; resta que en la figura seguent se conta per 10^a si hi a figura signifficativa. Si tant es que lo partidor non sie en l'orde en lo qual deu restar per raso. Semblantment hom deven scriure 0 si hom no ha desena detras e la figura de la qual se deu levar la premiera del partidor per que se pot levar 1^a vegada e las autras del partidor non se poden pas levar 1 vegada de las figuras que lur son desus. Car non hi a res que sie major que la figura del partidor que li es dejos et n'i a qualque una que es mendre que non pot aver dengun adjutors detras.

Item derrierament es de saber que aixi como las reglas del ajustar serveyssen

al multiplicar aixi meteis las reglas del substrayre serveyssen al partir. Car cada vegada que la premiera del partidor se leva la multiplicatio de la figura denotant quantas vegadas se leva contra la premiera figura del partidor se sustray de la summa que li era desus. Aprop la multiplicatio de la cascuna figura del partidor contra la figura del quociens que la premiera se sustray de la summa desus. Per que per prestament saber que resta desus en lo loc en que deu restar quant lo multiplicant las figuras del partidor per la figura del quociens que hom prenen la premiera hom pot escriure aquella multiplicatio en tal maniera que hom escriva lo simple de la multiplicatio dejos la figura del partidor §§ que se multiplica. Et si en la multiplicatio ha 10 ella se deu escriure detras un orde daves la part esquerra. Et aprop substrayre aquella multiplicatio orde par orde com es istat dit en lo capitol de sustrayre per que aprop que es partit no es autra causa propriment si non sustrayre tantas vegades lo partidor que en la summa que se partis non resta res et si res resta que sera mendre que lo partidor.

Qui aura feyt alcun

partiment & voldra provar si es ben feyt, que multiplicas lo nombre quociens quantas vegadas poden salhir per lo partidor a la qual multiplicatio ajusta so que restara si resta res. Car la summa que ne salhira deu esser semblant a la summa partida que s'appella quociens ho autrament lo partiment non valdria res.

Semblament quant hom ha feyta una multiplicatio. Et vol provar si es bona hom deu partir la summa de la multiplicatio per una de las 2 summas multiplicadas & parten per la 1, hom atroba l'autra si la multiplicatio es bona. Et ells non se son falhitz al partir. Et aixi atermena lo partir.

Car del doblar ni del mediar dels quals alcuns ne fan capitol expres, yeu no ne fatz cap de special. Car doblar es multiplicar per 2. Et mediar es partir per 2. Et per so non son pas capitols aixi com hom ditz.

Aprop que yeu hey tractat dels nombres entiers ho dels 5 capitols precedens resta que per complir lo nombre entier que yeu doni la cognoyssensa del 6. Que es per saber trayre la raditz dels nombres entiers.

Per la qual plus leugierament entendre yeu voli ensenhar quals son los nombres que han raditz donant la rason per que se appellan per lur nom. Aprop que es aquella raditz ni que vol dire trayre la raditz. Et

aprop yeu pausarey la[s] reglas necessarias assaber trayre la raditz.

Et per lo premier es de saber que los vocables de las mesuras & de las figuras que propriament son en la quantitat continua de la qual tracta geomatria per alcuna senblansa. Et troban et se unsan en la quantitat discreta de la qual es arismetica que es art de nombre. Per que per entendre quals son los nombres que an raditz premierament es necessari de entendre los vocables generals de las figuras de geomatria las quals pausarey aissi ab lurs figuras. Per las quals entendre deves saber que aquellas que son totas plenas son grossas segont aquella forma en que son feytas.

Et los vocables son aquestz quantitat continua generalment. Et devesis se en [3] partidas so es en ??? linea pla et espes.

Linea es que es longa sens largesa la qual atermena en puntz endevesibles.

Per la que se appella superficias es que ha lonc et larc de la qual los termes es linea. Spes que se appella cors es que ell ha lonc, larc, espes del qual los termes es linea dreyta & linea corba. Com son aquestas aissi pausadas, lo pla ha quasi infinitas partidas. Car alcuns son circulars. Com es aquest ◯. Alcunas son trianglars

como es aquesta ▽ Et aixi de totas aquellas que non an si no angles en qualz los sien feytas. Las autras son quadriangulars. Com es aquesta ▭ Et aixi e totas las autras que an 4 angles enquamna [?] maniera que sien feytas mas que sien plus longas que largas. Las autras son cayradas com es aquesta □ Et appella se cayrada car es tant larga como longa.

manuscrich: Ani N'i a autras que an 5 angles com es aquesta . Et aixi hom pot continuar en aquestas figuras sens fin segont los angles. Lo cors que es la terza partida general senblantment quasi infinidas partidas. Car alcunas son de tot redonas et se appellan esperica com es aquesta ^o.

Autras que se appellan piramidals et son aquellas que son largas dejos & agudas desus. Et aquestas son infinidas. Car alcunas son redonnas dejos com es aquesta . Alcunas an 3 angles com es aquesta . Autras que an 5 angles per aquesta maniera [*]Et * aixi continuant sens fin segont los angles dejos.

Autres son que son cayratz mas que son plus lonx que larcx com es

aquest . Autres son que son de tot cayratz com es aquest que son engoals que son tant larx como lonx, et tant d'espes como de larc.

Et appellan se cors cubitz com es aquesta autras son que son longas et redondas que se appellan columpnas que n'y a quasi infinidas segont que las diversifican en los angles.

Et per totas aquestas figura es de saber que totas las lineas  se redusissen en la dreyta.

Et totas las figuras plenas hom las redusis tant quant hom pot al veray cayrat per la raditz cayrada.

Et totas las figuras corporals se reduyssen tant quant hom pot al cors ho a la figura cubita et aysso per raditz cubita.

Et ayxi appropeys que significan los vocables generals de las figuras de geumatria. Per que es necessari de veser com se atroban per los nombres. Per so deves saber que nos avem nombre linar & es que es lonc como qui acomensa ad 1 et continua per ajustament de 1 pausant l'un aprop l'autre como qui pausava 6 per aquesta maniera IIIIII. Et aixi seguent tant quant hom

voldria. Autras son a maniera de pla et son que an lonc & larc et d'aquestas son quasi infinidas figuras. Car alcunas son circulars et son los nombres que venen de 5 & de 6. Car tostemps termenen en 5 o en 6.

Autras son angulas & d'aquestas son quasi infinidas figuras. Car alcunas son triangulars, car pausiem que sien per lurs unitatz fan la forma de un triangle et deu aver totztemps tantas unitas a [la] un costat como a l'autre. Como 3 que lo pausarie aixi et 6 per aquesta maniera et 10 aixi . Et senblantment de totz los autres trianglars, lo quals son infinitz. Alcuns son quadrianglars & son que an lonc & larc & son plus longas que largas. Et son totz los nombres que venen per la multiplicatio de 2 nombres engoals & totztemps lo nombre d'aquells 2 nombres que se multiplican es lo larc. Et lo major es lo lonc como 12, qui los pausa per aquesta maniera 3 es lo larc et 4 es lo lonc. Et qui los pausarie en aquesta maniera 6 es lo lonc & 2 es lo larc. Et aixi dels autres per ells se appellan quadriangulars. Car pausatz per lurs unitatz fan 4 angles com es dit.

Autres son de tot

cayratz e es tot nombre que ve per la multiplicatio de qualques nombre que multiplica si meteys com es 9 , que ve quant 3 multipliquen si meteys. Et aixi meteys totz nombre cayratz. Car pausatz que sien per lurs unitatz fan figura de tot cayrada en pla como 9 pausatz aixi et 16 per aquesta maniera . Et aixi aprop que tantas unitas an en larc como en lonc.

Autres son que an 5 angles coma 5 aissi et aixi sens fin segont lo creyssement dels angles.

Item son autres nombres que son corporals. Car son per maniera de cors que an lonc & larc & espes[6] et son totz los nombres que venen per la multiplicatio de 3 nombres semblants o desenblants. Et an de lonc & de larc & d’espes segont los nombres que se multiplican et son quasi infinitz. Car alcuns son de totz redontz & se appellan nombres esperitz et son los nombres que venen de 5 et de 6. Aprop que passan los cayratz los quals se appellan nombres esperitz per rason de lur terminatio. Car totztemps se term[in]en en 5 & en 6. Autres son piramidals et d'aquels son infinidas partidas segont las unitas que an dejos. Car si ells ne an 3, son triangulars

como aissi . Si an 4 quadriangulars et aissi sens fi. Autras ni ha que son cayradas mas que son plus longas que largas ni espessas et son los nombres que venen per la multiplicatio de 3 nombres engoals et si n'i a 2 engoals que lo tertz los sie engoal.

Et aquestz poden esser infinitz segont la diversitat dels 3 nombres que se multiplican.

Autres son que son cayratz en tota cayradura que se appellan nombres cubitz et son aquells que venen per la multiplicatio de 3 nombres senblantz, o per la multiplicatio de un nombre multiplicat en si meteys & una vegada en son cayrat que es tot un non remens que lo parlar sie divers.

Per que sapias que tot lo nombre cubit es contengut per 3 nombres engoals. Lo premier per lo lonc. Lo segont per lo larc. Lo tertz per l'espes. Et aquestz nombres abasten per las senblansas de las figuras de geomatria per los quals nombres propausatz generalment es de saber que totz los nombres superficials se redusissen tant quant hom pot al veray cayrat per la raditz cayrada.

manuscrich: redisissen Et totz los nombres corporals se redusissen tant quant hom pot als cubitz per la raditz cubita. Car dengun nombre ha veraya ni perfieyta raditz sinon aquells 2 nombres so es lo cayrat et lo cubit

Aprop que yeu hey demostrat en qual maniera las figuras generals de la quantitat continua de las quals tracta geometria se atroban per alcuna senblansa en los nombres. Et ay dit quals son los nombres que an veraya raditz. Resta que yeu ensenhe que es aquella raditz.

La radiz dels nombres cayratz es lo nombre la qual multiplica en si meteis multiplicat fay tant com es en lo nombre del qual hom vol aver la raditz. Per eyssemple la raditz de 25 es 5. Car multiplicant si meteis fay 25 & aixi dels autres.

La raditz dels nombres cayratz es la regla desus dita.

La raditz del nombre cubit es lo nombre del qual la multiplicatio del as son cayrat tant como lo nombre delqual hom vol aver la raditz cubita como per eyssemple la raditz de 27 es 3. Car multiplicant en 9, que es son cayrat, fay 27, del qual volia la raditz & aissi dels autres.

Aprop que yeu hey dit que es la raditz dels nombres que an raditz devi dire que vol dire trayre la raditz dels nombres que [no?] an raditz.

Trayre la raditz cayrada del nombre prepausat sies cayrat o de major cayrat contengut de dins aquell nombre, es cercar lo nombre lo qual multiplicat en si meteis

fay tant com lo nombre del qual hom vol la raditz cayrada.

Trayre la raditz cubita del nombre prepausat sies cubit o del major cubit contengut dedins aquell nombre es cercar lo nombre lo qual multiplicant ab son cayrat fay tant como lo nombre del qual hom vol aver la raditz cubita.

Resta que yeu pause las reglas que son per trayre las radises. Aprop que yeu hey demostrat quants son los nombres que an raditz et que es aquella raditz.

Tot premierament direm d'aquella que es per trayre la raditz cayrada per la qual miels ho poyres entendre. Et per aver la practica plus presta es de saber que hom deu devesir las figuras del nombre delqual hom vol aver la raditz cayrada de 2 en 2 acomensant las de devesir a la part dreyta como si devesian de 3 en 3[10]. Et lo contar es aital que 2 figuras fassan 1 orde, sien significativas o non. Et si lo nombre de las es par, per qu'es resta 1 figura sola a la part esquerra, aquella figura sola fara 1 orde. Et quant traytas la raditz acommensa a la part esquerra devisidas que sien la figuras com es dit en lo premier orde que daves la part esquerra. Et los autres ordes

continuant daves la part dreyta. Item deves saber que cada nombre es como la fin de nombre per que trasent la raditz hom comparan solament cascun orde aixi que resta de las precedens si res resta.

Et la comparacion es que las figuras se prenen como en lo contar per simpla 10 desenal centenal etc. Et aixi continua daves la part esquerra.

Aprop aquest notable se segueys la regla que es tala.

Escriut que sie lo nombre per sas figuras & devisidas que ellas sien per orde que son de 2 en 2. Hom deu sustrayre lo major cayrat que sie en lo premier orde escrivent so que restara desus figura per figura si ell no es cayrat & servar apart la raditz d'aquell cayrat sostreyt.

Aprop hom deu cercar la figura que es multiplicada en si meteyssa en la doble de la premiera raditz la sua multiplicatio se apropia mais a la summa del segont orde & de so que resta del premier, si res resta la qual multiplicatio se deu sustrayre del segont orde. Et d'aquo que restava del premier si res restava escrivent desus so que restara figura per figura. Et la figura dita sia raditz del segont orde per que se deu metre davant la raditz del premier orde. Et per aquella maniera hom deu continuar 1 orde aprop autre cercant las figuras que son multiplicadas

en si meteyssas. Et en lo doble de la raditz de totz los ordes precedens que se appropian mais de la summa d'aquell orde. Et de so que resta d'aquells autres sustraent las multiplications de las summas desus & metent la raditz davant las autras davers la part dreyta entro atant que hom aja tantas figuras per la raditz com hom aura del orde.

Et per major evidencia de la regla & de la practica, lo son de notar 4 causas.

La 1 es que per fin que la multiplicatio de las figuras que se multiplican ellas meteyssas. Et aprop lo doble de las precedens si una multiplicatz continuar lo devon escriure la figura davant lo doble de la raditz en tal maniera que aquella figura fassa lo premier loc daves la part dreyta. Et aprop deven multiplicar totas aquellas summas per hom la poden metre desus o dejos autra vegada per en multiplicant.

La 2 causa que es de notar es quant la multiplicatio dita per la figura significativa de 1 montarian mais que hom non voldria. Lavetz deu hom metre 0 per la raditz d'aquell orde, aprop continuar com es dit.

La 3 causa que es de notar es que si non resta res desus que aquell nombre es cayrat. Et si resta res lo deu esser mens que lo doble de la raditz o engoal que se es deve

quant non ni falh si non 1 de esser cayrat.

La 4 causa que es de notar es car 1 es principi et fondament de tot nombre que es cayrat. Et si resta res lo deu esser mendre el ha que ell ten lo premier loc de cascun orde dels nombres que prenen la senblanza de las figuras de geumatria per que 1 pot esser raditz et cayrat & cubit. Et per so deu hom usar de tant de quant es necessaria. Como de las autras figuras prenent la per raditz & cayrat &cubit.

Et per major declaratio de la regla et de totz los vocables & per demostrar la practica voli trayre la raditz de 2574937 devisidas las per orde e son 4 ordes. Aras sustray lo major cayrat que sie en los 4 orde que es la figura de 2, lo cayrat es 1, per que resta 1 sobre lo 2. Et tenem 1 per raditz del premier. Aras per lo 2, met 6 davant 2, que es lo doble de la premiera radiz que es 1, monta 26, que deves multiplicar per 6, que es la figura meteyssa pausa monta la multiplicatio 156, que deves sustrayre de 157 que es lo segont orde et so que restava del premier, resta 1, sobre los 7. Et aixi podes cognoysser que qui aurie presa autra figura que lo agra pauc ho trop montat. Per que devem metre 6 davant 1 et

tendrem 16 per la raditz d'aquells dus ordes. Item per lo tertz que metria figura significativa davant 32 que es lo doble de la raditz dels premiers ordes que montarian trop car al mens lo montaria 321, desus no ha que 149, per que devem metre 0 per raditz del tertz orde. E tendrem per raditz dels 3 ordes 160. Item per lo derrier orde met 4 davant 320 que es lo doble de la raditz dels autres ordes montan 3204, que deves multiplicar per 4 que es la figura pausada, monta la multiplicatio 12816 que deves sustrayre de 14937, que es lo derrier orde. Et so que restava dels autres resta en la sustractio 2121, per que tenen per raditz del quart orde 4, que deves metre davant 160. Et per conseguent la raditz del major veyray cayrat contengut en lo nombre propausat es [1604].

Et qui voldria esprovar si la raditz es ben treyta, que multipliqua la raditz trobata per si meteyssa, e saubra qual es lo cayrat, al qual cayrat ajuste so que resta mas qu'es lo cayrat ell trobara la premiera forma prepausada si ell ha ben feyt, avisant se que so que resta non sie major que lo doble de la raditz. 1604 × 1604 = 2572816 + 2121 = 2574937 (ámbe 2121 < 2 × 1604 = 3208) Et qui non ha trobaria lo premier nombre propausat aquo

lo sie senhal quall ha mal feyt car aisso es la vertadiera prova.

Aprop que yeu hey mes la regla et la practica de trayre la raditz cayrada convenient es que yeu pause la [raditz] regla et la practica de trayre la raditz cubita per la qual es de saber que hom deu devisir las figuras dels nombres dels quals hom vol aver la raditz cubita de 3 en 3 comensant a la part dreyta aixi com al contar per tal que 3 figuras fassan un orde que sien signifficativas o non & si es cas que las figuras non se puescan metre de 3 en 3 so que restava sie 1 o 2 daves la part esquerra & sera 1 orde como si ere complit lo ternari. Et divisidas que sien las figuras com es dit aquell ternari que es daves la part esquerra se appella lo premier orde sie complit o non. Et continuant vers la part dreyta et cascun orde es per maniera de si de nombre.

Perque non se comparan si non aysso que resta del premier si tant es que res reste. La comparansa es aquella del nombrat tot aysso notant.

E scriut que sie lo nombre et devisidas que sien las figuras per lurs ordes que son de 3 en 3 com es dit hom deu sustrayre lo major nombre cubit que sie en lo premier orde escrivent

desus so que restara si ell non es cubit & servar apart la raditz d'aquell cubit sustreyt.

Aprop per lo segont orde, hom deu cercar per raditz la figura de la qual summa que ve per ella per la maniera que s'en siec se apropia a las figuras del segont orde & de so que resta del premier, si es res restat, la maniera del cercar la summa es aquesta que deu hom metre la figura davant la raditz del premier orde per tal maniera que la raditz premiera sie 10.

Et per aquell nombre ho deu hom multiplicar lo triple de la raditz.

Aprop segondament mais autra vegada deu hom mais multiplicar la summa de la multiplicatio feyta per la figura pausada davant la raditz del premier orde a la multiplication.

Tersament deu hom ajustar lo cubit de la figura pausada en tal maniera que lo simple del cubit fassa lo premier simple per la summa per que sie en lo cubit ha 10 & ella sie ajustada ab lo simple de la 2 multiplicatio. Et la summa derrierament atrobada que mais se apropia se deu sustrayre de las figuras del 2 orde & d'aquo que resta del premier orde. Et aixi hom ha la raditz d'aquels dus ordes premiers

per lo tertz & per totz los autres ordes senblament deu hom cercar la figura de la summa que ve per ella, como es dit e per aquella maniera que totjorn hom deven metre la figura de davant la raditz atrobada per aquell nombre multiplicat lo triple de totas las figuras atrobadas per raditz.

Aprop la summa de la multiplicatio segondament deu hom multiplicar per la figura jon [?] la pausada davant la raditz. Aprop ajustar tersament lo cubit de la figura como es dit del segont orde sustraent la summa atrobada de la summa desus servat las figuras apart per lurs ordes entro atant que per cascun orde hom aja 1 figura per raditz. Et lo nombre que fan aquellas figuras mesas o pausadas per orde seguent estadas atrobadas es la raditz d'aquell nombre de la qual lo volian la raditz cubita si non resta res en la raditz del nombre major cubit que sie contengut en lo nombre perpausat.

Et per evidencia major es de saber que la 2^a et la 4^a causa notadas aprop la raditz regla de la raditz cayrada en aquest loc fan a perpaus. Et si non son neccessarias per que sufisca que sien scriuta 1^a vegada aplicans

las ai perpaus del cubitz.

Et es de saber que quant non resta res que lo nombre es cubit. Et si resta res pot esser mendre o engoal o major del triple de la raditz

A major declaratio de la regla et de la practica voli trayre la raditz cubita 4 913 087. Divisis las son 3 ordes aras sustray lo major cubit del premier orde que es 1 et restan 3 sobre los 4 et tenent per la raditz del premier manuscrich: davat orde. Per lo segont met 7 davant la raditz trobada que es 1, monta 17 per que per la premiera multiplicatio multiplica 3 que es lo triple de la raditz trobada per 17 monta 51. Item per la seconda multiplicatio multiplica 51 per 7 que es la figura prepausada monta 357 a la qual summa deves ajustar lo cubit de 7 que monta 343. Et deves fer que 3 fassan lo premier loc per que deves ajustar los 4 ab los 7. E aprop los 3 ab los 5 montan totas las summas 3931error: montan 3913 que deves sustrayre de 3913 que es lo segont orde et so que restava del premier et no resta res sobre aquells dus ordes que tenen 17 per la raditz d'aquells 2 ordes.

Item per lo 3 qui metria denguna figura significativa davant 17 ia montarian de mais sens fer la multiplicatio que non

fa lo 3 orde e que non ha si non 87 per que per la raditz ? metren 0 e tenem la raditz del major cubit que sia en la summa perpausada 170 e resta 87 &c.

Et qui voldra provar si ha ben feyt trayra la raditz cubita que aja lo sieu cubit & aprop ajuste so que restara & atrobara la premiera summa si ben ho a feyt autrament non. Et aysso es la veraya prova. Car lo es istat dit que totz los nombres sobrefficials sien redusitz tant quant hom puesca als cayratz per la raditz cayrada & totz los autres nombres corporals se redusestan als cubitz per la raditz cubitz.

Et que dengun nombre no ha perfieyta ni vertadiera raditz sinon los cayratz et los cubitz.

Per tant lo se siec per rason que de tot nombre hom pot cercar la raditz cayrada perfieyta si es cayrat, ho enperfieyta si non es cayrat. Et la raditz cubita perfieyta si es cubit. O enperfieyta si non es cubit.

Aprop que hey ensenhat de trayre la raditz perfieyta, resta que deven ensenhar de trayre las radises enperfieytas que son per totz los nombres que non son cayratz ni cubitz. Et aquo segont

la comparansa de la raditz so volem la cayrada o la cubita.

Et per so deves saber que tot nombre que non ha perfieyta raditz es contengut entre 2 nombres que an perfieyta raditz las 2 raditz son 2 nombres propdans so es lo major sobremonta lo menor solament de 1. Com appar qui pren la raditz de 2 cayratz & 2 cubitz propdans et car tot nombre mejancier conte lo nombre menor entierament que ha la raditz en 1^a partida o diversas partidas del major propdanament seguent que la raditz per conseguent es neccessari que la raditz enperfieyta del nombre mejancier contenguda la raditz del menor entierament, e una partida o diversas partidas de que monta mais la raditz del major que aquella del menor per que la raditz imperfieyta dels nombres entiers non pot esser sens nombre rot.

Per aprop que yeu aurey tractat dels nombre per sos capitols yeu darey la practica de cercar la raditz enperfieyta. Et ayxi aprop que tot nombre pot esser raditz perfieyta & que tot nombre non ha pas raditz perfieyta.

Et aixi termenan los 6 capitols los quals complidament tractan dels nombres entiers com appar en

lurs lox. Segueyssen se las provas de la practica per los 5 capitols pausatz que se fan per 1^a figura simpla.

Car practica presta alcunas vegades plays aytant como art longa & a la hom layssa l'art & se retorna hom a la practica.

Non remens que las provas de l'art ha pausadas en lur locx de ellas meteyssas sien seguras & mot profitablas car ellas son longas. Yeu voli ayssi pausar 3 provas communas las quals son de practica & non pas d'art per que ellas poden falhir com yeu demostrarey las quals 3 provas se fan per aquest 3 nombres 9, 7, 3, dels quals davant que yeu doni la maniera yeu voli donar la rason per que hom provan miells per aquels 3 nombres que per los autres.

Sapias que aixi com es istat dit en lo capitol del contar.

Lo premier nombre complit que sie es 10 et car 9 es lo major nombre que sie dedins 10 per l'autesa que ell ha escriven per 1 figura et es ordenat per provar los autres nombres, lo nombre de 3 provas per rason car es entierament en 9 & es partida entiera de 9 et per so quant aquella de 9 falh & aquella de 3 falh.

Et quant aquella de 7 es bona aquella de 3 es bona. La rason per que 7 prova es la desconveniensa que ell ha ab los nombres que son dejos 10. Car aixi com un juge que garda justicia non deu aver conveniencia ni ajustansa ab degun per tal que per ajustansa non corrumpa son jujament et aixi 7 tot solet non ha conveniencia ni ajustansa ab degun nombre que sie dejos lo nombre de 10. Et totz los autres hi an conveniencia como cascun pot veser de 2 ab 4, de 3 ab 6, de 4 ab 8, de 5 à 10. Et aixi resta que non an conveniensa ab degun per que ell es juge de tot los autres, lo qual jujament se appella provar.

Aprop que yeu hey dit per que aquells 3 nombres provan los autres resta que yeu done la practica.

Et deves saber que totz 3 poden provar per 1^a regla & per una maniera meteyssa per que aquesta es la regla general.

La prova de cascuna d'aquellas 3 figuras la cascuna prenen per si et de totz nombres que se poden partir entierament per ellas es pausada chifra. Et so que non es complidament lo nombre que partis daquels 3 nombres es la prova. Exemple de cascuna de 3: 3, 6, 9, 12. Tot son chifras de 9: 9, 18, 27, 36, 45, 54. Tot son chifras de 7: 7, 14, 21, 28 , tot son (0) et aixi s'entent

de totz autres nombres. Item per so que no es 3 entierament: 1 et 2 es de 1 entro a 2. Item so que no es 9: es de 1 entro a 8. Item so que no es 7: es de 1 entro a 6.

Autra regla per 9 et per 3.

Item deves saber que la prova de 9 se fay plus prestament ajustant las figuras como si eran simplas que fay partent et non remens lo ve tot ad una prova. Perque 9 falh prestament. Et per so se siec que car 9 ha familiaritat et convenensa ab 2 contraris so es ab lo ajustar de las figuras simplas & lo partir que leugierament ab son jujament que es la sieua prova. Car mais que lo reste lo nombre de las unitatz de totas las figuras per fas simplas partiscan per 9, aquella summa de dreyt he ( ho?) a l'envers aixi hom mudan las figuras, de tot jorn vendra 1^a prova et senblantment que las ajustara. Per eyxemple partis 358 al dreyt o a l'envers que ne fassas 853 o las mudes aixi com te vulhas, o ne leva de la una e met en l'autra. Et aprop partis ho ajusta las 3 figuras car tot jorn vendra 1^a prova. Et aixi es de tota autra summa & senblantment lo deven attendre de 9 et 3.

Non quant 7 falh senblantment. Car tot nombre ha 943

familiaritat et conveniencia ab totz los nombres que pot partir entierament, per so remens que 7 sie lo plus disconvenient de las figuras ell ha familiaritat ab totz los nombres que ell pot partir entierament. Per rason delsquals ell pot fer avol jujament. Car qualques nombres sie qui li ajustaria o li levaria 7 o los deves familiars de qualque orde que sien mas que semblantment hom en fassan simples et desenas, la prova de 7 sera falsa car ella non se mudara pas com deurie fer per rason d'aquo que es ajustat o levat.

Et senblantment es de 9 & de 3 que qui los ajustaria o lo levaria o lurs familiars, o lur prova es falsa. Et aixi appar que aprop las provas del art las quals de ellas meteyssas non poden falhir.

La plus segura que sia per 1^a figura es aquella de 7. Et la plus leugiera es aquella de 3.

La segonda prova es quant 7 et 9 se acordan en falsetat.

Car avans que 7 et 9 se puescan acordar en falsetat es necessari de pausar o levar un dels nombres familiars a 7 et 9 dels quals lo minor es 63. En qualque orde que se vulhan lo plus segur que sie que non voldria fer las provas del art que prove per 7 et per 9. Car la un corrigira l’autre

si falhia. Si non que falhan per los nombres que lurs son familiars com es istat dit. Et aixi appar que 7 non pot provar si non partent et so que resta de la summa aprop lo partiment es la prova d'aquella summa partida, et 9 et 3 poden provar partent como 7 et ajustant las figuras prenent so que passa la figura per la qual hom prova et aquo passat hom deu ajustar ab la seguent figura prevenent tot jorn la prova com es dit.

Et non que non obstant tot aquo so que es dit d'aquellas 3 figuras per so non resta que 6 et 8 non puesquan provar las ancaras que son plus seguras que non es aquella de 9, et plus aquella de 8 que aquella de 6. Et volem provar como 7 per so qui vol provar per una figura que prove per aquellas 4 figuras si vol be esser segur. Car davant que sie aquo deu en falsetat fay mestier de ajustar o de levar un grant nombre. Car lo mendre es 504504 es lo mai pichin comun multiple de 9, 7 e 8 et nota que so que es dit de 7 & de 9, ses lurs senblans pot dire d'aquestas figuras so es lurs senblans & familiars.

Item sapias que tot nombre fora 2 & 5 pot esser prova partent mas que serai lonc si hi avia 2 figuras per nos ajudam de las 4 dictas figuras.

Siec se l'aplicacio de las provas ditas.

Aprop que yeu hey dit per aquellas figuras provant e la regla es mesa

de la maniera del provar. Et aixi demostrant com se poden falhir. La cascuna per si & de totas ensemps.

Resta que yeu aplique la maniera del provar en lurs capitols que se poden provar per aquels nombres simples.

La practica de provar lo ajustar.

Quant tu auras ajustat diversas summas & vols provar si as be feyt, & voles fer la prova per 7, tu deves la prova de cada summa adjustadas. Et aprop ajustar totas aquellas provas, et la prova de la summa que vendrá per lo ajustament de totas aquelas provas deu esser senblant a la prova de la summa major que es venguda per lo ajustament de totas las summas. Et si non se senblan lo ajustament feyt es fals. Per eyxemple, voli ajustar las 3 summas seguentz & aquellas 3 sien eyxemple general et per mais et per mentz.

Aras per 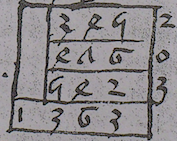provar si es be feyt premierament parteys 345 par 7, restent 2, que es la prova de la premiera. Item partis 476 par 7, resta 0, que es la prova de la segonda summa. Item partis 542 per 7, resta 3, que es la prova de la tersa summa. Aras ajusta aquellas 3, summas, montan 5, partis 1363 que es la summa se summa de

tot per 7, atrobaras que restan 5, per que lo ajustar es be feyt aprop que aquellas 2 provas se senblan. Senblament fey per 6 et per 8. Et qui vol provar aquel ajustament meteis per 9 ho per 3 que partisca la cascuna summa d'aquellas 2, ajustadas mas que de la prova de la premiera hom fassa como si era de la segonda. Et aprop continuant entro atant que aja la prova de la segonda de la qual fassa como si era de la tersa summa et aixi hom deven tenir si non la prova de la tersa en la qual son enclusas las autras & en aquellas deu esser senblant la prova de tota la summa.

Autrament ajusta totas las figuras de la premiera summa de tot jorn prenent solament so que passa 9 o 3, et aixi continuant entro atant que hom ajan prova de totas las figuras de las 3 summas manuscrich: laqua la qual deu esser senblant a la prova de totas las figuras de la major summa si eran ajustadas per la maniera dita.

Et es de notar que aquestas provas en lo ajustar ni en lo sustrayre non se poden aplicar si non en las causas desenblans per que aquellas causas desenblans hom deven provar cascun orde per si.

Item per provar lo sustrayre. Qui vol provar una sustractio feyta per 7, prenga la prova de las 2

mendres summas. Cada una per si. Aprop ajuste aquellas 2 summas o provas car la prova de la summa d'aquellas 2 provas ajustadas deu esser senblant a la provas de la major summa & senblantment es de 9 et de 3 que pendra la prova de las 2 mendres summas pertent ?o ajustant las figuras com es dit desus.

Per provar lo multiplicar

Qui aura feyt una multiplicacio & voldra veser si aura be feyt prenga las 2 provas de las 2 summas qui [si non] son multiplicadas, aprop multiplica aquellas 2 ensems. Car la prova de la multiplicacio d'aquellas 2 provas seran senblant a la prova de la summa de la multiplicatio feyta si es be feyta. Et aquellas 2 provas se prenen pertent ho ajustant com es dit.

Nota en lo multiplicar & en lo partir practica. Per la qual practica en lo provar del multiplicar hom pot fer una crotz & als 4 angles hom met las provas segont que yeu direy aras la maniera.

Premierament en lo multiplicar en l'angle dejos hom deu metre la prova de una de las summas multiplicadas, et en l'angle desus hom deu metre la prova de la multiplicatio d'aquellas 2 provas se deven metre en l'angle de la crotz

daves la part dreyta. Et en l'angle de la part esquerra se deu metre la prova summa de la multiplicatio feyta. Et si las provas que son als angles de la part esquerra & de la part dreyta senblan a la multiplicatio feyta es bona la prova, autramentz no.

Per provar lo partir te regla

Qui aura feyt un partiment & voldra lo provar, premierament pause la prova del partidor en l'angle dejos de la crotz. Et en l'angle desus meta la prova de la summa que es venguda per lo partir aprop multiplique aquellas 2 provas & la prova d'aquella multiplicatio ajuste ab la prova de so que resta desus. Et la prova d'aquella derriera summa meta en l'angle de la crotz daves la part dreyta & en l'angle daves la part esquerra meta la prova de la major summa partida & si aquellas 2 provas que son a la part dreyta et a la part esquerra son senblans lo partiment es bo, autrament non.

Per provar la raditz cayrada

Qui aura feyt una raditz cayrada & vol provar si ha be feyt prenga la prova d'aquella raditz & a la prova del cayrat de la raditz ajusta la prova de so que resta de sus car la prova d'aquella derriera manuscrich: sum summa deu esser senblant a la prova de la summa de la qual es treyta la raditz si es be treyta, autrament ella es mal treyta.

Per provar la raditz cubita

Qui aura treyt una raditz cubita de un nombre & vol provar si ha be feyt prenga la prova d'aquella raditz trobada & ajuste la prova de so que resta a la prova del cubit de la prova de la raditz. Car la prova d'aquella derriera summa que ve per lo ajustament de la prova del cubit & de la prova de so que resta deu esser senblant a la prova de la major summa de la qual hom ha treyt la raditz. & si non son senblantz, la raditz es mal treyta.

Et aixi la practica dels 4 capitols passatz ab lur provas del art en lurs locx pausatz et las provas de la practica ayssi derrieramentz pausadas segont los capitols que volen esser provatz. Per que es complida en nom de jesus la premiera partida.

Siec se la segonda partida d'aquesta compendi que parla de nombre rot. Et premierament que e nombre rot et de que tracta.

Per saber & aver cognoyssensa del nombre rot lo qual es necessari diversas de vegadas a fer rasons de mercadaries & de diversas autras causas.

Premierament deves saber que es

nombre rot. Nombre rot es so que non es un entier & so que no ha rason de un entier. Car pren la denominacio de las partidas en las quals se deviseys lo un entier.

Et per so deves saber que en tal nombre rot ha 2 nombres & la un se escriu desus l'autre ab una linea en mieg.

Et lo desus se appella nombrador & aquell dejos se appella denominador. Com si yeu volie escriure $\frac{3}{4}$ faria en tal maniera $\frac{3}{4}$. Et deves saber que lo nombrador que es desus es rot.

Et lo denominador que es dejos es totztemps en un entier et so que non es un entier es rot com es dit en la devesion dessus pausada.

La maniera de escriure nombre rot

Et per so que d'aquest nombre rot hom puesca aver cognoyssensa yeu demostrarey & ensenharey de redusir 2 ho diverses nombres rotz a un denominador et aprop de ajustar et de sustrayre & de multiplicar & de partir & de mediar & de trayre la raditz.

Lo premier capitol que ensenha que es redusir & la maniera de redusir.

Per saber redusir diverses nombres & §§

Per saber redusir diverses nombres rotz a un denominador deves saber premierament que causa es redusir.

Redusir es 2 o diverses nombres rotz desenblantz metre los en 1 denominador comu per fer los senblantz. Per la qual causa saber fer lo son 2 reglas generals per gardar se de pena.

La 1^a es redusir 2 nombres rotz en 1 denominador.

La 2^a es per redusir 3 o tropis nombres rotz en denominador.

Multiplica lo nombrador del un par lo denominador de l'autre, et aprop los denominadors ensemps si n'i a mais de un et so que vendra quant multiplicaras los 2, denominadors sera lo denominador comu. Et so que vendra del nombrador ab lo denominador de son contrari se deu escriure sobre lo nombrador. Et aysso sera lo nombrador et ayssi atrobam nombrador novell et denominador novell.

Et ayssi se fa per maniera de cors. Per eyssemple voli redusir $\frac{2}{3}$ et $\frac{4}{5}$. Et multiplicarey lo nombrador del premier que es 2 per 5 que es denominador del segont et fan 10, que escriurey sobre los 2. Aprop multiplicarey 4 per 3 que es son contrari que fan 12, que pausarey sobre los 4 aprop multiplicarey

los 2 denominadors so es 3 per 5, que fan 15 que pausarey quasi en lo mieg de los 2 denominadors et aixi los $\frac{2}{3}$ son $\frac{10}{15}$ et los $\frac{4}{5}$ son $\frac{13}{15}$, lo exemple de la practica.

Et si lo hi a entier ho entiers as los rotz a redusir, premierament lo denominador multiplica los entiers per lo denominador de son rot, a la qual multiplicatio hom deven ajustar lo nombrador & tota que aquella sera nombrador & l'autre es perdent.

Eyssemple voli redusir 2 $\frac{1}{3}$ et $\frac{4}{5}$. Premierament multiplica 2 entiers per 3, es denominador de son rot, e fan 6. Ajusta la 1 que es lo nombrador e son $\frac{7}{3}$. Aras redusis $\frac{7}{3}$ & $\frac{4}{5}$ com es dit desus montan los $\frac{7}{3}$ $\frac{35}{15}$. Et los $\frac{4}{5}$ montan $\frac{12}{15}$.

Item que voldria redusir 3 $\frac{1}{2}$et 4 $\frac{2}{3}$, premierament deu redusir los entiers en son rot & dire per lo premier 2 vegades 3 son 6 & 1 son $\frac{7}{2}$. Item per lo segont deu dire 3 vegades 4 son 12 & 2 son $\frac{14}{3}$. Aras redusis $\frac{7}{2}$ per $\frac{14}{3}$.

Item qui vol redusir entiers solets ab rotz solets los entiers se deven multiplicar per lo denominador del rot. Eyssemple voli redusir 7 entiers soletz & $\frac{2}{3}$, multiplica

7 per 3, son $\frac{21}{3}$ et es feyt.

Item qui vol redusir entiers soletz ab entiers & totz tot ensemps premierament deu metre los entiers en son rot. Aprop multiplicar los entiers en son solet per lo denominador del rot. Exemple voli redusir 7 entiers soletz & 3 $\frac{2}{3}$, e direy premierament 3 vegades 3 son 9 & 2 fan $\frac{11}{3}$. Aprop direy 3 vegades 7 fan 21 & es feyt.

Et per aquesta maniera se fan totas las reductions que son en que volia si no 1 o 2 nombres rotz que se fa per aquesta maniera [per la] premiera regla & §

La 2 regla general que es per redusir 3 ho diverses nombres rotz a 1 denominador es aquesta que hom deu atrobar 1 nombre en que se atroben entierament aquells nombres rotz et quant hom los a atrobatz hom ho deu partir per cascun denominador et so que ne ven hom deu multiplicar per lo nombrador del denominador que aura partit. Exemple voli redusir $\frac{1}{2}$ $\frac{2}{3}$ $\frac{3}{4}$ $\frac{5}{6}$. Totz aquells nombres rotz se atroban en 12, partis 12 per 2 & venen ne 6, multiplica 6 per 1, fan 6, que son $\frac{6}{12}$ per $\frac{1}{2}$. Item partis 12 per 3 et venen ne 4, los quals multiplica per 2,

fan 8 que son $\frac{8}{12}$ per $\frac{2}{3}$. Item partis 12 per 4 & venen ne 3, los quals multiplica per 3 & fan 9 que son $\frac{9}{12}$ per $\frac{3}{4}$. Item partis 12 per 6 que ne venen 2 que deves multiplicar per 5 que fan 10, que son $\frac{10}{12}$ per $\frac{5}{6}$. Et es feyt.

La regla per atrobar totz los nombres rotz que se deven redusir.

Multiplicar totz denominadors so es los dus premiers et so que ne vendra multiplica per lo tertz et aprop so que vendra per lo quart & aixi dels autres. Et en lo nombre que que se atrobam per la multiplicatio del derrier denominador se atrobaram tot los rotz entierament qui ho voldra atrobar. Eyxemple voli atrobar 1 nombre en lo qual se atroban entierament $\frac{1}{2}$ $\frac{1}{3}$ $\frac{1}{4}$ [$\frac{1}{5}$] que direm 2 vegades 3 fan 6. Item 6 vegades 4 fan 24. Item 24 vegades 5 fan 120. Et en 120 a entierament $\frac{1}{2}$ $\frac{1}{3}$ $\frac{1}{4}$ $\frac{1}{5}$ lo $\frac{1}{2}$ son 60, lo $\frac{1}{3}$ son 40, lo $\frac{1}{4}$ son 30, lo $\frac{1}{5}$ son 24 & es feyt.

Per atrobar mendre nombre en lo qual hom atroban entierament totz los rotz que hom vol atrobar, hom deu gardar si dengun dels denominadors es contengut entierament en l'autre, ho en alcuns dels autres. Com es 2 et

entierament en 4 & en 6. Et en totz autres nombres pars et 3 es en 6 et en 9. Et 4 es en 8 & en 12. Et senblanment dels autres. Et fa vegada devem layssar aquells que son contengutz et premier aquells que contenen.

Exemple voli atrobar 1 nombre en que se atroben entierament $\frac{1}{2}$ $\frac{1}{3}$ $\frac{1}{4}$ $\frac{1}{6}$ $\frac{1}{8}$. Et dire 2 es en 4 et 3 en 6 et 4 en 8. Et per so yeu layssarey 2, 3, 4 et pendrey 6 & 8 et diriey 6 vetz 8 son 48. Et ha ne entierament $\frac{1}{2}$ $\frac{1}{3}$ $\frac{1}{4}$ $\frac{1}{6}$ $\frac{1}{8}$. Per atrobar lo mendre nombre.

Item per mais abreviar et qui be se ajustara per atrobar lo menor nombre en que se atrobian entierament totz los rotz qui los voldra atrobar, hom deu ajustar & avisar se per la multiplicatio dels menors si atroban los majors. Aixi quant lo multiplicant 3 per nombre per so fan 6^nas. Et quant lo multiplicant es 4 per nombre par fan 8^nas. Et quant lo multiplicant es 5 per nombre par hom fan 10^nas. Et ayssi dels autres. Et la vegada hom deven layssar los majors & pendre los menors

Exemple. Voli atrobar un nombre en que hom atrobian entierament

$\frac{1}{2}$ $\frac{1}{3}$ $\frac{1}{4}$ $\frac{1}{5}$ $\frac{1}{6}$ $\frac{1}{8}$ $\frac{1}{12}$ $\frac{1}{216}$. Et de totz aquetz denominadors yeu non pendrey si non 2, 3, 5 et 8. Car qui multiplica 3 per 2 fan 6^nas et qui multiplica 5 per 6 que es nombre par fan 10^nas. Et direy 2 vegades 3 son 6. Et aprop 6 vegades 5 fan 30. Et qui multiplica per 30 que es nombre par fara 16^nas. Et per so direm 8 vegadas 30 fan 240 et en 240 se atrobam totz les nombres rotz desus pausatz.

Nota per redusir los rotz dels rots.

Item sapias que la premiera d'aquestas 3 practicas de atrobar lo nombre es bona per redusir los nombres rotz. Car en lo derrier nombre que se atroba en la maniera desus dicta se atroban como per exemple.

Voli atrobar un nombre en que se atroban $\frac{2}{3}$ de $\frac{1}{5}$ et $\frac{2}{4}$ de $\frac{1}{2}$ multiplica totz aquels 4 de nombradors. Car en lo nombre que ne salhira es so que hom vol. Et aissi entendatz de totz los rotz et aixi se complis la reductio.

Lo capitol que ensenha de ajustar nombre rot. Premierament es mestier de saber que es nombre rot ni que vol dire ajustar nombre rot.

Ajustar nombre rot es 2 o diverses rotz dels quals degun de ells

non fey 1 entier metre los ensemps per saber si volem 1 o diverses entiers et si ajustatz non fan un entier quina partida son de un entier que se apropia mais al compliment de 1 entier que degun dels per solet no fasia. Car en nombre non se fa ajustament si que las causas que si ajustan sien senblantz per ajustar diverses nombres rotz.

Et ha hi 1^a regla general que es tala:

Redusis totz los nombres rotz a 1 denominador per lo qual capitol de la reductio las quals reductions totas ensemps partis per lo denominador comu et sera feyt.

Exemple voli ajustar $\frac{2}{3}$ et $\frac{3}{4}$. Premierament redusis la premiera regla [lacuna] ajusta 8 et 9 fan 17, partis per 12 [lacuna] que ne ve 1 et $\frac{5}{12}$.

Item voli ajustar $\frac{1}{2}$ $\frac{2}{3}$ $\frac{3}{4}$ $\frac{5}{6}$. Premierament se deu redusir per la seconda regla $\frac{1}{2}$ $\frac{2}{3}$ $\frac{3}{4}$ $\frac{5}{6}$. Ajusta 6, 8, 9, 10 que son 33, partis per 12 que ne ve 2 et $\frac{9}{12}$. Et aixi lo ajustar sobre lo redusir non fa si non levar los entiers si hi son.

Lo tertz capitol que ensenha de sustrayre nombre rot es levar una partida de un entier de sa senblant o de una major

o de un entier per saber si resta res quina partida de un entier resta. Et de quant val mais la una partida que l'autra.

Car en ? nombre non se pot fer substractio ni cognoysser de quant es major un nombre que un autre si non aquells sien senblantz per so que hom sapian sustrayre en nombre rot.

Et ha 2 reglas generals. La premiera regla per sustrayre la summa que se deu sustrayre & la summa de la qual se deu sustrayre se deven redusir a un denominador comu. Aprop sustrayre lo mendre nombre dels dus redusis de la major et dejos aquo que restara metre lo denominador comu.

La 1 regla per sustrayre quant sera neccessari de sustrayre nombre rot de un entier solet o de un entier ab un rot ensemps lo entier se pausa & se conta per tant com es lo denominador comu.

Et nota que hom se deu be ajustar que quant hom ha diverses rotz de part lo nombre que se deu sustrayre o de partir [?] de paert del cascun que de totz aquels que son de una part, hom deu fer una summa. Et aprop la sustractio com es dit. yeu voli pausar un exemple per plus carament ajam las reglas desus dictas. Et ajan miells

la practica. Voli pausar los exemples.

Et premierament voli sustrayre un nombre rot de un rot., so es $\frac{2}{3}$ de $\frac{3}{4}$. $\frac{3}{4}$ - $\frac{2}{3}$ = $\frac{9}{12}$ - $\frac{8}{12}$ = $\frac{1}{12}$ Redusis $\frac{3}{4}$ son $\frac{9}{12}$ et $\frac{1}{12}$[. Et] son $\frac{8}{12}$, leva 8 de 9 resta $\frac{1}{12}$. Et per aquesta maniera se sustray un rot de un rot.

Item si de 2 o de tropis voliam sustrayre 1 hom ho fa per aquesta maniera. Voli sustrayre $\frac{1}{2}$ + $\frac{2}{3}$ - $\frac{3}{4}$ = $\frac{6}{12}$ + $\frac{8}{12}$ - $\frac{9}{12}$ = $\frac{14}{12}$ - $\frac{9}{12}$ = $\frac{5}{12}$ $\frac{3}{4}$ de $\frac{1}{2}$ [e] $\frac{2}{3}$. Redusis totas aquellas partidas, se atroban en 12. La $\frac{1}{2}$ et $\frac{2}{3}$ de 12 son Error, legir $\frac{14}{12}$ $\frac{5}{14}$ e los $\frac{3}{4}$ de 12 son 9, leva 9 de 14, restan $\frac{5}{12}$.

Et par aquesta maniera se leva un rot de tropis.

Item voli sustrayre de un rot solet tropis rotz como de $\frac{3}{2}$ voli $\frac{1}{2}$ et $\frac{1}{5}$. Redusis aquestas partidas que se atroban en 20, los $\frac{3}{4}$ de 20 son 15, la $\frac{1}{2}$ et lo $\frac{1}{5}$ de 20 son 14, leva 14 de 15, restan $\frac{1}{20}$ et per aquesta maniera se sustrahen diverses rotz de 1 rot solet.

Item voli sustrayre de 2 rotz com de $\frac{1}{2}$ et $\frac{2}{3}$ voli levar $\frac{1}{4}$ et $\frac{2}{5}$. Redusis totas aquellas partidas son ?? la $\frac{1}{2}$ et los $\frac{2}{3}$ de? son ??la $\frac{1}{4}$ et los $\frac{2}{5}$ ?? montan 39 ???

Per aquesta maniera se fay qui vol sustrayre

diverses rotz de diverses rotz.

Item voli sustrayre de un entier solet 1 rot com de 1 voli sustrayre $\frac{1}{3}$. Redusis lo 1 entier e val 3 leva 1 de 3 resta $\frac{2}{3}$ & per aquesta maniera se leva de 1 entier 1 rot solet.

Item voli sustrayre de 1 entier 2 rotz. Com de 1 entier levar voli $\frac{1}{2}$ & $\frac{1}{3}$; redusis totas aquellas partidas se atroban en 6; pausa 6 per lo 1 entier. Aprop lo $\frac{1}{2}$ & lo $\frac{1}{3}$ de 6 son 5, leva 5 de 6 resta $\frac{1}{6}$. Et per aquesta maniera se fa qui vol levar de 1 entier tropis rotz.

Item voli sustrayre de 1 entier ab rot ensemps rot de 1, entier, he $\frac{1}{2}$ voli levar $\frac{3}{4}$. 1 + $\frac{1}{2}$ - $\frac{3}{4}$ = $\frac{8}{8}$ + $\frac{4}{8}$ - $\frac{6}{8}$ = $\frac{12}{8}$ - $\frac{6}{8}$ = $\frac{6}{8}$[ = $\frac{3}{4}$] Redusis & pren 8, & lo entier pausas, & aprop la mitat $\frac{1}{2}$, & son 12. aprop pren los $\frac{3}{4}$ de 8 e son 6, leva 6 de 12, restan $\frac{6}{8}$. Et per aquesta manuscrich: 12 maniera se fa qui vol levar de 1 entier & 1 rot o diverses 1 rot ho tropis &c.

Lo 4 capitol que ensenha de multiplicar en nombre rot.

A multiplicar en nombre rot es de saber que es multiplicar en nombre rot. Multiplicar en nombre es de cercar si tota la summa que se deu multiplicar, coven a tot

denominador del nombre multiplicant segont aquella proporcio que cove al nombrador multiplicant. Et per so per saber metre en practica es una regla general.

  Multiplica nombrador per nombrador et denominador par denominador per la practica que son 2 causas de notar.

La 1 es que nombre entier solet es nombrador sens denominador, et per so quant se multiplica per lo nombrador del rot el pren lo denominador del nombre que lo multiplica.

Item 2 es de notar que lo nombre entier ab lo nombre rot que l’entier se deu metre en lo rot & fer ne nombrador ajustant li lo nombrador premier.

Et per donar la maniera pausi los exemples. Si voles multiplicar nombre per rot com es $\frac{2}{3}$ × $\frac{3}{4}$ = $\frac{6}{12}$ [= $\frac{1}{2}$] $\frac{2}{3}$ per $\frac{3}{4}$, multiplica 2 per 3, fan 6, aprop multiplica 3 per 4, fan 12, los quals deves pausar de jos 6 & son $\frac{6}{12}$. Et aixi fay dels autres & pausant que ni aguessa diverses. Com si volia multiplicar $\frac{2}{3}$ × $\frac{3}{4}$ × $\frac{4}{5}$ = $\frac{24}{60}$ [= $\frac{2}{5}$] $\frac{2}{3}$, $\frac{3}{4}$, $\frac{4}{5}$, deven dire 2 vegades 3 son 6, aprop 6 vegades 4 son 24, aprop 3 vegadas 4 son 12, et 5 vegades 12 son 60. Et aissi ne ve $\frac{24}{60}$.

Et sapias que per aquesta maniera se pot

saber quant monta lo rot del rot. Como qui demandaria quant montan los $\frac{2}{3}$ dels $\frac{2}{5}$ de $\frac{1}{4}$. Montan $\frac{4}{60}$. Et aixi dels autres.

Item voli multiplicar nombre entier & rot ensemps per nombre solet. 3 $\frac{2}{3}$ × $\frac{3}{4}$ = ($\frac{9}{3}$ + $\frac{2}{3}$) × $\frac{3}{4}$ = $\frac{11}{3}$ × $\frac{3}{4}$ = $\frac{33}{12}$ [=$\frac{11}{4}$] Com 3 $\frac{2}{3}$, per $\frac{3}{4}$. Premierament redusis los entiers[*] et digas [*] & fets ne rotz 3 vegades 3 son 9, et 2, fan $\frac{11}{3}$. Aras multiplica los 2 nombradors et digas 11 vegades 3 son 33, aprop multiplica los denominadors et digas 3 vegadas 4 fan 12, que deves metre dejos 33, fan $\frac{33}{12}$, que deves metre entiers & son 2 & $\frac{9}{12}$.

Item si tu voles multiplicar nombre entier et rot per entier. Com es 3 3 $\frac{3}{4}$ × 4 $\frac{2}{3}$ = $\frac{15}{4}$ × $\frac{14}{3}$ = $\frac{210}{12}$ = 17 $\frac{6}{12}$ [= 17 $\frac{1}{2}$] $\frac{3}{4}$ per 4 $\frac{2}{3}$. Premierament redusis los entiers en son rot & digas per lo premier, 4 vegades 3 son 12, & 3, fan $\frac{15}{4}$. Aprop digas per lo segont manuscrich: vedas 3 vegadas 4 son 12, & 2 son $\frac{14}{3}$. Aras multiplica 15 per 14, montan 210. Aprop digas 3 vegades 4 son 12, & son $\frac{210}{12}$, met los entiers que son 17 et $\frac{6}{12}$.

Item si tu voles multiplicar nombre entier solet per entier & rot. Com es 7 per 3 et 7 × 3 + $\frac{2}{3}$ = 7 × $\frac{11}{3}$ = $\frac{77}{3}$ = 25 + $\frac{2}{3}$ $\frac{2}{3}$. Premierament redusis lo entier en son rot, et digas 3 vegades 3 son 9.

et 2 , fan $\frac{11}{3}$. Aras multiplica 7 per 11, montant 77, que son $\frac{77}{3}$, met los entiers que son 25 & $\frac{2}{3}$. Autramentz multiplica 7 per 3 entiers 7 × 3 + $\frac{2}{3}$ = 21 $\frac{2}{3}$ = 21 $\frac{14}{3}$ = 21 + 4 $\frac{2}{3}$ = 25 $\frac{2}{3}$ son 21. Aprop multiplica 7 per 2 fan 14, met entiers son 4 & $\frac{2}{3}$, ajusta ab los 21 & son 25 et $\frac{2}{3}$.

Item si voles multiplicar nombre entier solet per nombre rot solet com es 7 per $\frac{2}{3}$, multiplica 7 per 2, fan 14/3, met entiers son [4] et [$\frac{2}{3}$] et es feyt.

Et deves saber que non son diversas manieras de multiplicar que hi aja nombre rot sinon aquellas 5 manieras pausadas. Si non que las volguessan mudar davant et aixi meteys vendria a un nombre.

Lo 5 capitol que ensenha de partir que hi aja nombre rot.

Partir per nombre rot es cercar si la summa pueys que sufficientment yeu hey frasi incorrecta ensenhat de multiplicar en nombre rot.

Resta que yeu ensenhe de partir. Et premierament direy que vol dire partir.

Deves saber que partir per nombre rot es cercar si manuscrich: comuement la summa que se deu partir es comunement al contador del nombre partidor segont aquella proporas que cove a son denominador. Et si lo partidor es nombre entier es acercar si la summa que se deu partir en la qual ha nombre

rot cove a tot lo partidor segont aquella proportio cove a un entier per que non que tostemps partir sien en entiers ho en rotz. Et es acercar que cove a un entier. Et per so que hom ho sapian be partir quant hi aura nombre rot depart lo partidor ho depart la summa que deu partir, ho depart de cada un.[?] es una regla general de partir lo nombre rot.

Redusis ton partidor & la summa que se deu partir a un denominador, aprop partis com si eran entiers.

Et per donar la practica pausarey 6 exemples segont que en 6 manieras se pot usar lo partiment del nombre rot.

[1] Si tu voles partir nombre rot per nombre rot, com es aissi $\frac{3}{4}$ per $\frac{3}{4}$ ÷ $\frac{2}{3}$ = $\frac{9}{12}$ ÷ $\frac{8}{12}$ = $\frac{9}{8}$ = 1 $\frac{1}{8}$ $\frac{2}{3}$, tu deves premierament redusir a un denominador et son los $\frac{3}{4}$: $\frac{9}{12}$ et los $\frac{2}{3}$ son $\frac{8}{12}$, partis aras 9 per 8, ne ve 1 et $\frac{1}{8}$.

Et si volies partir $\frac{2}{3}$ per $\frac{3}{4}$, quant auras redusit, partis 8 per 9, & serian $\frac{8}{9}$.

Item 2^ment si voles partir nombre entier ab nombre rot per nombre rot solet, com es 3 $\frac{3}{4}$ per $\frac{2}{3}$, premierament redusir l’entier en son rot, disent 4 vegades 3 son 12, et 3, fan $\frac{15}{4}$. Item redusis ho tot a un denominador et digas 3 vegades 15 son 45. Aprop 4 vegades 2 fan 8, aras partis 45

per 8, que ne ve 5 & $\frac{5}{8}$.

Item 3^ment si voles partir nombre entier & rot. Per entier & rot. Com es aixi 7 $\frac{3}{4}$ per 3 & $\frac{2}{3}$, premierament 7 $\frac{3}{4}$ ÷ 3 $\frac{2}{3}$ = $\frac{31}{4}$ ÷ $\frac{11}{3}$ = $\frac{93}{12}$ ÷ $\frac{44}{12}$ = $\frac{93}{44}$
= 2 $\frac{5}{44}$ redusis los entiers per son rot et digas 4 vegadas 7 son 28, et 3 fan $\frac{31}{4}$. Item 3 vegadas 3 son 9 & 2 fan $\frac{11}{3}$. Aprop redusis ho tot a un denominador comu et digas 3 vegadas 31 son 93. Item 4 vegadas 11 son 44, partis 93 per 44, ne ve 2 et $\frac{5}{44}$ e es feyt.

Et qui voldria fer aquest partiment per lo contrari ne vendria $\frac{44}{93}$. Item 5^ment voli partir nombre entier solet per nombre rot. Com 7 per 3 $\frac{2}{3}$, 7 ÷ 3 $\frac{2}{3}$ = 7 ÷ $\frac{11}{3}$ = $\frac{21}{3}$ ÷ $\frac{11}{3}$ = $\frac{21}{11}$ = 1 $\frac{10}{11}$ . premierament redusis l'entier ab son rot, & digas 3 vegades 3 fan 9, et 2 fan $\frac{11}{3}$. Aprop digas 3 vegades 7 son 21. Aras partis 21 per 11 que ne ven 1 et $\frac{10}{11}$. Autrament quant los entiers et rotz per entier solet com es ayci 7 et $\frac{3}{4}$ per 3. Premierament redusis lo entier ab son rot et digas 4 vegades 7 fan 28, et 3 fan 7 $\frac{3}{4}$ ÷ 3 = $\frac{31}{4}$ ÷ 3 = $\frac{31}{4}$ ÷ $\frac{12}{4}$ = $\frac{31}{12}$ = 2 $\frac{7}{12}$ . $\frac{31}{4}$. Aprop redusis ton partidor et digas 4 vegadas 3 fan 12. Aras partis 31 per 12, que ne ve 2 et $\frac{7}{12}$. Autrament quant los entiers se poden partir per lo entier. Premierament partis los entiers et so

que resta redusitcom es dit, exemple en los cas desus dit, parteys 7 & $\frac{3}{4}$ per 3. Premierament partis que ne ve 2 & resta 1 que deves partir ab $\frac{3}{4}$ per 3. Et per so digas 4 vegades 1 & 3 son 12 et 3 fan $\frac{7}{4}$. Aprop digas 4 vegades 3 son 12. Aras partis 7 per 12, que ne ve $\frac{7}{12}$. Ajusta ab lo premier partiment que son 2 et $\frac{7}{12}$.

Item 6^ment si tu voles partir nombre rot solet per entier solet com es $\frac{2}{3}$ ÷ 3 = $\frac{2}{3}$ ÷ $\frac{9}{3}$ = $\frac{2}{9}$ $\frac{2}{3}$ per 3, premierament redusis ton partidor & digas 3 vegades 3 fan 9. Aprop partis 2 per 9 ne ve $\frac{2}{9}$ et es feyt .

Et per aquesta se fan totz los partimentz que se poden fer ont ha nombre rot.

La prova de lo que es dit desus de multiplicar et del partir et del ajustar et del sustrayre.

Si tu voles provar si as be feyt quant tu auras partit ho multiplicat. Sapias que lo es una regla general que lo multiplicar prova lo partir. Et lo partir prova lo multiplicar.

Et tot retorna en lo premier istat ab lo denominador comu. En loqua[l] sie feyta la reductio.

Et per so si tu voles provar quant auras feyta una multiplicatio, partis so que ne

ve en 1 de las summas que tu as multiplicat. Et quant tu par[tis] una ]?] tu atrobaras l'autra. Exemple multiplica $\frac{2}{3}$ per $\frac{3}{4}$ fan $\frac{6}{12}$, partis per $\frac{2}{3}$ tu atrobaras que ne ve $\frac{3}{4}$, et si tu par[tis ?] $\frac{6}{12}$ per $\frac{3}{4}$, lo ne vendra $\frac{2}{3}$ si has be feyt.

Per provar lo partir.

Si tu voles provar quant tu auras partit si tu as ben feyt, multiplica so que ne ve per ton partidor, car so que ne vendra de la multiplicatio sera la summa que auras partit. Exemple partis $\frac{2}{3}$ per $\frac{3}{4}$, ne ve $\frac{8}{9}$. Prova: multiplica $\frac{8}{9}$ per $\frac{3}{4}$, monta $\frac{24}{36}$, que valen $\frac{2}{3}$.

Plus presta regla.

Partis lo nombrador [per] lo denominador comu et so que ne vendra sera la summa que tu has partida. Aprop partis lo denominador particular per lo denominador comu et so que ne vendra sera la summa que era ton partidor. Exemple: partis $\frac{2}{3}$ per $\frac{3}{4}$ et ne ve $\frac{8}{9}$. Prova: partis 8 per lo denominador comu que es 12, ne ve $\frac{8}{12}$ que valen $\frac{2}{3}$ que auras partit. Aprop partis 9 per 12 ne ve $\frac{9}{12}$ que valen $\frac{3}{4}$ que era lo partidor.

Et si hi avia per lo partidor entier ho entiers, el se deu retornar en son rot. Aprop prova com es dit. Exemple: partis $\frac{3}{4}$ per $\frac{2}{3}$ ne ve 1 & $\frac{1}{8}$, son $\frac{9}{8}$, partis 9 per lo denominador que es 12, ne ve $\frac{9}{12}$ que valen $\frac{3}{4}$, que

es istada la summa que auras partit.

Aprop partis 8 per 12 que ne ven $\frac{8}{12}$, que valen $\frac{2}{3}$, que era ton partidor.

Et aixi appar la maniera de provar la multiplicatio et lo partiment en nombre rot.

Et senblantment lo ajustar per lo sustrayre. Et lo sustrayre prova lo ajustar.

Car lo es regla general que la un contrari prova l’autre.

Per saber abreviar lo nombre rot. Car diversas vegades aprop partiment restan nombres rot mot petitz com serian $\frac{2}{4}$, $\frac{6}{8}$, $\frac{3}{4}$, $\frac{6}{8}$.

Per so per retornar a plus grosses nombres 1 regla es so es que hom deu atrobar un nombre per lo qual lo se puescam partir entierament lo nombrador & lo denominador. Et so que vendra manuscrich: nominado nominador sera denominador.

Et qui non sabere atrobar lo major nombre per lo qual se poden partir engoalment prenga aquells que saupra atrobar & continue tant qu'ell non puesca plus atrobar autre nombre lo qual se puesca partir. Exemple pausi $\frac{3}{4}$, $\frac{6}{8}$, pode veser que 36 & 48 lo cascun se pot partir per 2 per so partis 36 per 2 que ne ve 18, aprop per los 48 que ne ve 24 e son $\frac{18}{24}$. Item partis 18 per 2 ne ve 9, aprop partis 24 per 2 ne ve 12 et son $\frac{9}{12}$. Item 9

& 12 se poden partir per 3, partis donx 9 per 3,ne ve 3, aprop partis 12 per 3, ne ve 4 et son $\frac{3}{4}$. Per que $\frac{36}{48}$ valen $\frac{3}{4}$. Et ayso agra pogut cercar & fer per 3 & per 4 & per 6 & per 12. Et quant plus grant nombre hom pren tant mais val. Et sapias que cascun nombre pot partir si meteys. Com si disie 3 de 3 quantas vegadas ne pot falhir 1.

Per cognoysser si lo nombre se pot abreviar et hom no ho sap et hom ho vol saber cal es lo major nombre per lo qual se pot abreviar. Aquesta es la regla.

Partis lo denominador per lo nombrador et si resta res retorna partir lo 2 denominador per lo 2 nombrador. Et l’autra vegada resta res torna partir lo 3 denominador per lo 3 nombrador .

Et per aquesta maniera tu continua entro atant que tu tropias un nombrador que sera un 1, ho atrobaras 1 denominador que partira entierament son nombrador. Et si tu atrobaras lo nombrador que es 1 d'aquell nombrador non se pot

abreviar mas es mestier que demore en aquella maniera. Et si atrobas lo denominador que partis entierament son nombrador aquell denominador es lo major nombre per lo qual plus prestament aquell nombre rot se pot abreviar.

Per so hom de usar com es dit desus en la premiera regla.

Assaber la valor del nombre rot.

Car es necessari que vol dire nombre rot et tropis han desir de saber ho. Et per so ne doni 1 regla general, so es assaber que hom multipliquen lo nombrador per la valor de so que es & so que ne vendra hom partiscam per lo denominador. Exemple voli que valhen 3 defait multiplica 3 per la valor de 1 escuts & sie la valor 21 gros, monta 63, partis per 4, ne ve 15 & restan $\frac{3}{4}$ quartz que multiplicarie per la valor de 1 gros et sie la valor 15 deniers, direy 3 vegadas 15 son 45,per 14 ne ve 11 .d. $\frac{1}{4}$, valen doncas $\frac{2}{4}$ defait 15 gros 11 .d. $\frac{1}{4}$. Et aixi entendas de totas las autras causas que se multiplican per la valor de so que son.

Pratica per saber doblar & mediar.

Aprop que ay dit de la multiplicatio & del partiment, resta que yeu diga del doblar & del mediar de que alcuns ne fan capitol. No remens que no ho sien, yeu ne doni una regla general: qui voldra doblar, multiplique per 2.

Et qui voldra mediar que partisca per 2. Senblantment qui voldra triplar , que multiplique per 3.

Et qui voldra aver lo 3 que partisca per 3.

Et aixi s’entent dels autres.

Per autra practica presta dona tala maniera de doblar & de mediar. Si vols doblar multiplica lo nombrador per 2 ho partis lo denominador per 2, si es nombre. Per exemple,dobla $\frac{1}{4}$, digas 2 vegadas 1 son $\frac{2}{4}$. Autra maniera, partis 4 per 2, ne ve $\frac{1}{2}$. Et aixi se fa lo triplar et totz los autres. Exemple de triplar $\frac{1}{6}$. Digas 3 vegadas 1 son $\frac{3}{6}$. Autra maniera partis 6 per 3, ne ve $\frac{1}{2}$. Et aixi fay de totz los autres multiplicant lo nombrador ho partent lo denominador per 2 si es nombre par o multiplica lo denominador per 2. si tu voles mediar,lo nombrador per 2 Exemple media $\frac{2}{3}$, ne ve $\frac{1}{3}$. Autra maniera multiplica 3 per 2, son $\frac{2}{6}$. Item media $\frac{1}{4}$, multiplica 4

per 2 ne ve $\frac{1}{8}$, senblantment fassa qui voldra aver lo tertz lo $\frac{1}{4}$ partent lo nombrador o multiplicant lo denominador.

Lo capitol que ensenha de trayre la raditz en nombre rot.

Resta aras derrierament
per donar fi et conclusio ab nombre rot d’ensenhar de trayre la radix per la qual causa es nescessari de dire quals son los nombres que an raditz.

Aprop pausarey la regla per trayre aquella raditz.

Per lo premier que es per saber quals son los nombres que an raditz.

Deves saber que aixi com es istas dit non nombre que ha raditz. En los nombres entiers tant solament los nombres cayrats & cubitz an raditz.

Perque los nombres rotz cayrats & cubitz solament an raditz, per que veram que es nombre rot cayrat & nombre cubit. Aprop las deffinicions mesas en los entiers que es nombre rot cayrat expecialment.

Nombre rot cayrat es aquell del qual lo nombrador & lo denominador son nombres cayratz. Com son $\frac{4}{9}$, o que abrevias que siez retornatz que lo nombrador & lo denominador son cayratz como son $\frac{8}{18}$, lo qual nombre

abreviat retorna en $\frac{4}{9}$.

Que es nombre rot cubit. Specialment nombre rot cubit es tot nombre del qual lo nombrador & lo denominador son nombres manuscrich: nombretz cubitz com son $\frac{8}{27}$, o que abreviatz que sien retornan que lo nombrador & lo denominador cubitz como son $\frac{16}{54}$ lo qual nombre abreviatz retornan en $\frac{8}{27}$. Nota per aquetz 2 nombres que an raditz, es de saber que tot nombre mendre es partida o partidas de tot autre nombre major & per so totz los nombres cayratz menors son partida o partidas cayradas dels majors nombres cayratz. Et totz los nombres cubitz menors son partida o partidas cubitas dels majors nombres cubitz.

Et per conseguent dengun nombre rot non es cayrat ni ha raditz veraya cayrada si non quant qualque nombre mendre cayrat es nombrador de qualque nombre cayrat major. Si non que los nombres cayra[t]s sian entiers et rots ensemps. Et la vegada lo menor cayrat denomina lo major, ni degun nombre rot non es cubit ni ha raditz cubita si non qualque nombre cubit menor sie nombrador de qualque nombre

cubit major. Si non que lo nombre sie entier et rot tot ensemps. Et la vegada lo major cubit pren denomina del menor cubit. Et per tal que lo sie plus clar com los nombres mendres cayratz et cubitz son partida o partidas o cubitas dels majors cayrats o cubitz.

Pausi aissi una figura cayrada contenent 36 partidas engals cayradas la qual figura per aquesta maniera feyta representa los nombres cayrats de 36 la qual figura es aquesta:

En la qual hom pot veser que 1 e 4 [e 9] et lo cascun d'aquels 3 nombres es partida cayrada de la qual figura car 1 es $\frac{1}{36}$ & 4 es $\frac{1}{9}$ et 9 son $\frac{1}{4}$, & 16 & 25 [non] son partidas ]cayradas] car non se poden retornar en 1 partida. Com es feyt en las autras. Car 16 non se pot atrobar si non a $\frac{4}{9}$ et 25 ni se poden res abreviar. Et non rementz son cayratz ho fan figura cayrada dedintz la figura de 36 como aprop en la figura. Et per aquest exemple se deu entendre de tots los autres cayratz et cubitz.

Car tot nombre cayrat es contengut per 2 nombres engoals. Et tot nombre cubit per 3. Siec se car los nombres rotz an 2 nombres que los nombres rotz cayratz son contengutz per 4 nombres so es per 2 engoals lo nombrador et per 2 autres engoals lo denominador & los nombres cubitz son contengutz per 6 nombres so es per 3 engoals lo nombrador et per 3 autres lo denominador. E deves saber que ni en los [cayratz] ni en los cubitz jamais los nombres dels denominadors ni son egoals et los nombres dels nombradors. Car quant lo nombrador es menor que lo denominador son majors que aquells que contenen lo nombrador.

Et quant lo denominador es menor que lo nombrador que se esdeven quant lo nombre cayrat ha cubit e ha entiers ho rotz ensemps nombres que contenen lo nombrador son majors que aquells que contenen lo denominador.

Que son las [ra]dises generalment.

Aprop que yeu hey dit quals son los nombres que an raditz yeu son contreyt que yeu diga que es aquella raditz. Per que aprop las deffinitions pausadas als

entiers que aytant se convenen als rotz como generals que ellos son.

Las especials son que es la radiz cayrada especialment.

La raditz cayrada del nombre rot son 2 nombres dels quals la multiplicatio de la un multiplicat en si metey[s] fa tant como es lo nombrador. Et la multiplicatio de l'autre fay tant com es lo denominador del nombre cayrat.

Que es la raditz cubita especialment? La raditz cubita dels nombres rotz son 2 nombres dels quals la multiplicatio de la 1 multiplicat en son cayrat fa tant com es lo denominador et la senblant multiplicatio de l'autre fa tant com es lo nombrador del nombre rot cubit. Et aixi appareys que cascun nombre cayrat & cascun nombre cubit ha 2 raditz una per lo nombrador et l'autra per lo denominador.

Que es trayre la raditz cubita?

Trayre la raditz cubita en nombres rot es cercar los 2 nombres dels quals las multiplications que proveneyssen

Que vol dire trayre la raditz del nombre rot generalment?

Aras 3 devi de mostrar que vol dire trayre la raditz per que anem per replicar so que n'es istat dit en los entiers.

Que vol dire trayre raditz cayrada especialment?

Trayre la raditz cayrada en nombre rot es de cercar los 2 nombres del quals las multiplications que provenisson quant lo cascun dels es multiplicat en si meteys se apropian mais del nombre prepausat la 1 del nombrador et l'autra del denominador?

Que es trayre la raditz cubita?

Trayre la raditz cubita cayrada en nombre rot es servar los 2 nombres dels quals las multiplications que preveneyssen quant lo cascun dels es multiplicat prepausat la una del denominador & l'autra del nombrador. Et aixi aprop que quant hom tray las radis que si lo nombre non es cayrat ho cubit que hom extray la raditz del major nombre cayra[t] o cubit que sie contengut en lo nombre prepausat en mais en figura. ? figura entiera com es aquella desus la qual ha totas sas partidas entieras.Ò

Resta que aprop que yeu hey dit quals son los nombres que han raditz & qual es aquella raditz ni que vol dire trayre

la raditz yeu doni la regla per la qual son alcunas causas davant per notar.

La 1, que lo son alcuns nombres rotz com es istat dit en las deffinicions dels nombres cayratz & cubitz que restan en lur nombrador & en lur denominador. No hi a veraya raditz mas que las abrevia et los retornan que ajan veraya raditz o me [?] aqui meteys es istat dit per exemple en los cayratz de $\frac{8}{18}$ que retornan en $\frac{4}{9}$ en que los cubitz $\frac{16}{54}$ que retornan en $\frac{8}{27}$ los quals nombres non remens que ells sien diverses en nombres, ells son totz uns en valor car aytant valen manuscrich: $\frac{8}{9}$ $\frac{4}{9}$ como $\frac{8}{18}$ et $\frac{8}{27}$ como $\frac{16}{54}$. Et per so quant los nombres rotz non han raditz si els se poden abreviar autramentz non mas layssar ?? los en lur premier istat.

Non remens que se puescan abreviar en autres nombres que non han raditz.

Item 2^tament es de mostrar que si solament lo nombrador & lo denominador non an raditz que jamais d'aquell[s] nombres non auriam la veraya raditz car ell non ha vertadiera raditz. Aprop aquestz 2 notables la regla de la raditz es tala.

Regla per trayre la raditz: de la raditz

del nombrador fay nombrador et de la raditz del denominador fay denominador et sera feyt per la practica d'aquesta regla.

Et deves saber que las radises del nombrador & del denominador se prenen aixi com als entiers.

Et per major evidencia de cascuna raditz pausarey 2 exemples. 1. Per aquells que han raditz quant son abreviatz.

Exemple per los cayratz que an raditz.

$\sqrt{\mathrm{<math><mfrac><mn>4</mn><mn>9</mn></mfrac></math>}}$ = $\frac{2}{3}$ Voli la raditz de $\frac{4}{9}$. Et digas la raditz de 4 son 2 per lo nombrador. E la raditz de 9 son 3 per lo denominador. Perque la raditz de $\frac{4}{9}$ son $\frac{2}{3}$.

Exemple per los cubitz. $\sqrt[3]{\mathrm{<mfrac><mn>8</mn><mn>27</mn></mfrac>}}$ = $\frac{2}{3}$ Voli la raditz de $\frac{8}{27}$. Et digas la raditz de 8 son 2 per lo nombrador. Et la raditz de 27 es 3 per lo denominador, et aissi la raditz de manuscrich: $\frac{4}{9}$ $\frac{8}{27}$ son $\frac{2}{3}$.

Exemple per los cayratz que si abrevian. Voli la raditz $\frac{8}{18}$, abrevia la, tornant en $\frac{4}{9}$. Per so digas la raditz de 4 es 2 per lo nombrador, Et la raditz de 9 es 3 per lo denominador et aixi la raditz de $\frac{4}{9}$ son $\frac{2}{3}$ et per conseguent de $\frac{8}{18}$, per so car la un val tant como l’autre.

Exemple per los cubitz que se abrevian. Voli la raditz de $\frac{16}{54}$, abreviada retornant en $\frac{8}{27}$, la raditz de 8 es

2 per lo nombrador et la raditz de 27 es 3 per lo denominador, & aixi la raditz de $\frac{8}{27}$ es manuscrich: son $\frac{16}{54}$ $\frac{2}{3}$ et per conseguent la un val tant como l’autre.

Per aplicar la regla cant hi a entiers tot ensemps.

Aquesta regla ab los exemples pausatz abasta a trayre tota raditz emperfeyta de nombres rotz car si lo nombre es entier et rot ensemps lo non cal mas que metre los entiers en son rot et fer ne nombrador ajustant li lo premier. Et aprop fer como es dit et treytas que sien las radises del nombrador & del denominador hom deu partir las radises del nombrador per las radises del denominador per tornar las en entier et sera feyt.

La prova si la raditz es ben trayta.

La prova de la raditz dels nombradors et dels denominadors se fay aixi. Com si eran nombre entier.

La regla per trayre la[s] [ra]ditz enperfieytas.

Et car a la fin del capitol que ensenha de trayre la raditz perfeyta en los nombres entiers ay dit que a la fin d'aquest capitol yeu demostra

de trayre la raditz enperfieyta deguda causa es que yeu demostre de cercar et de trayre la, segont que art e pratica vol.

Per la qual es util de dire quals son los nombres que an raditz enperfeyta ni que es aquella raditz ni per que es dita enperfieyta. Pausant per evidencia 2 conclusions ab lurs declaracions et proansas et aprop de donar la regla que es per donar la practica de saber trayre nota _☞ aquella raditz enperfieyta.

Quals son los nombres que an raditz enperfieyta. Per lo premier que es quals son los nombres es de saber que aixi com es istat dit en los nombres entiers & la reatat[?] en aquest capitol solamentz los nombres cayratz et cubitz an raditz perfieyta tant en los entiers com en los rotz. Perque totz los autres nombres an raditz enperfieyta. Et son propiamentz totz los nombres que non poden venir per la multiplicatio de qualque nombre multiplicat en si meteys ho en son cayrat. Et totz aytals nombres son contengutz entre 2 nombres prochans que an veraya et perfieyta raditz.

Que se appella nombres

cayratz o cubitz prochans. Son aquells los quals la raditz del major non sobremonta la raditz del menor si non de 1.

Semblantment es dels nombres rotz qui pren lo nombrador per si et lo denominador per si aras qui compara lo nombrador al denominador infinidas son las desconveniensas. Per que aysso abaste per saber quals son los nombres que an raditz enperfieyta en nombres entiers & en nombres rotz.

Per saber que es aquella raditz enperfieyta deves saber que car tot nombre es raditz perfieyta de 1 cayrat et de 1 nombre cubit que aquels que son ditz raditz enperfieyta.

Perque es dita raditz enperfieyta. Son ditz raditz enperfieyta per comparansa al nombre delqual volen aver la raditz. Et aquo es car lo cayrat et lo cubit perfieyt d'aquella raditz contan mais o mentz una o diversas partidas de 1 cayradas que lo nombre prepausat. Como appar qui fey las figuras. Como es feyta aquella desus segont que es la raditz per las quals visiblament lo deven demostrar si los nombres son cayratz o non. Et aixi dels cubitz per que aquestas

son las diffinicions de las radises enperfieytas.

Que es raditz enperfieyta cayrada?. Raditz cayrada enperfieyta es que multiplicat lo nombre en si meteys non monta pas a 1 mays o non deyssent pas a 1 mentz del nombre del qual es raditz enperfieyta.

Que es raditz cubita enperfieyta? Raditz cubita enperfieyta es nombre que multiplicat en son cayrat non monta pas a 1 ni deyssent pas a 1 mentz del nombre del qual es raditz enperfieyta.

Siec se per metre las conclusions.

Per major evidencia d'aquestas radises aysso son las 2 conclusions.

La 1^a conclusion es que jamais de dengun nombre entier contengut entre 2 nombres prochans que an raditz perfieyta hom non atrobaran la raditz perfieyta.

Lo premier notable.

Per aquesta conclusion son 2 causas de notar la 1^a que car totz los nombres mejanciers que tienen entierament lo menor dels 2 en respieyt dels quals son mejanciers & plus necessari es que lur raditz contenga la raditz entierament del menor & qualques causa de 1

que complis la raditz del major.

Per que se siec que lo es necessari que totas las radises dels nombres mejanciers sien entiers & rot ensemps.

La 2^a causa de notar es que la proprietat de multiplicar de nombre rot es que abreuge los entiers. Et si es rot solet que no hi aja entiers que la multiplication se aluenhe del compliment de 1 entier. Et tant quant mais se multiplica tant mais se aluenha. Et la rason per que appareys per la definicio del multiplicar de nombre rot.

La premiera prova de la conclusio.

Empossible es que la raditz que rot fassa cayrat o cubit que venga a nombre entier solet o pas totas las radices dels nombres mejanciers han nombre rot. Per que jamais dengun nombre entier & § la major se prova visablament per las figuras qui la fay segont la raditz. Et se prova per la multiplicatio del nombre rot ab lo segont notable. La major se prova per lo premier notable.

La 2^a prova.

Tota persona que vol la raditz perfieyta dels nombres entiers mejanciers

cerque que per la multiplicatio del nombre rot ab nombre rot venga nombre entier mas lo es empossible que la multiplicatio de nombre ab nombre rot venga nombre entier. Car enpossible es que jamays hom atrobe la raditz perfieyta dels nombres entiers mejanciers. La major es clara car los nombres son entiers et las radises an nombre rot per lo premier notable.

manuscrich: conglusio La 2^a conclusio.

Per bona raditz que hom aja, totztemps la podes aver plus propdana et milhor. Et non remens jamais hom non vendra a la perfieyta.

Lo premier notable.

Per la declaracio es dever que 1 es como quantitat continua que se pot metre en infinidas partidas ni se poden assignar las partidas en las quals derrierament 1 se pot metre la qual causa se manifesta per lo denominador la qual per grant que ell sie hom ne pot donar 1 major.

Et aixi com lo nombre entier non fi en augmentatio lo nombre rot no ha fi en diminutio. Car quant lo denominador creys et lo nombrador deminuis en valor,

Lo 2 notable.

Item mais deves saber que aixi com creis ho abrevian lo nombre rot hom

fan mais apropiar ho mais lunhar de 1 entier la multiplicatio.

Et quant lo prenen de la 1 que es rot tant mais se apropian del cayrat ho del cubit major

Et quant hom mens ne pren hom se bayssan mays vers lo menor.

Et aixi appar que hom lo poden fer creysser & abreviar las multiplicatio per mays apropiar se del nombre mejancier, qui lo vol.

La prova de las conclusions

La 2^a partida de la conclusio es clara per la premiera conclusio.

Et la 1^a partida se prova per tal rason, quant mais la multiplicas per son degut feyta se appropia del nombre que hom vol tant es milhor mas qualque multiplicatio que sie hom pot donar una autra que se appropiara mais per que per bona raditz que hom aja hom la pot aver plus prop e milhor. La major de si es clara e la menor se propiia per las 2 notabeles.

D'aquestas 2 conclusions ab lurs declarations deyssenden 2 corellaris.

Correlaris

Et lo premier corellari es que totz los nombres rotz cayratz & cubitz so meyns de 1. Et son contengutz entre dus nombres entiers cayratz o cubitz.

La prova

car non tant solament aquells mas totz las autres.

manuscrich: coerellari Lo 2 corellari

Non remens que los cayras et los cubitz dels nombres entiers non ajan fin en augmentatio mas son de nombres rotz cayratz et cubitz.

La prova que los cayratz et los cubitz entiers non ajan fin car las radises non an fin. Que los rotz sien mays. Car dejos 1 non fin en deminuent sobre 1. Car entre 2 nombres prochans son enfenitz nombres rotz cayratz et cubitz mejanciers.

Et aixi los nombres rotz son enfenitz en 3 manieyras. Una dejos 1 entier l’autra desus continuant. Et l’autra entre totz los mejanciers & los nombres entiers que non an mas una infinitat que es § augmentatio.

Et deves saber que aquest correllari ab sa declaratio signiffica que nombres rotz an mays de rason en tropis esser enfenitz que los nombres entiers.

Et non significa pas si los nombres entiers eran infenitz que los nombres rotz fossen mais car lo es contra rason.

Siec se per donar la regla.

Pueys que ey dit quals son los nombres que an raditz enperfieyta.

Digam que

es aquellas raditz ab las 2 conclusions.

Resta que yeu done la regla que dona la practica de trayre la raditz que es tala.

La regla per trayre la raditz enperfieyta.

De la raditz enperfieyta del menor cayrat [o] cubit ab alcunas partidas de 1 fay raditz. Et segont que la multiplicatio montara o deyssendra et tu creys ho abrevia las partidas del 1. Car de tant mens montara o devallara la multiplicatio.

Et per declaratio d'aquest regla et de la practica se de saber que lo es melhor de pendre la raditz que non pas mas 1 que lo nombre del qual es raditz que non es de pendre aquella que non fa pas 1 mentz.

Quar rason que es mais es plus manifest. Et si ve plus clarament que so que es mens.

Et car aquellas 2 radises son compausadas de 2 nombres rotz que deven esser prochans o de 2 partidas propdanas de 1 nombre per saber quals son aquells nombres & aquellas partidas. Et per atrobar las, ab mens de pena son alcunas causas de notar.

La 1^a es que los nombres rotz an natural progressio en augmentatio & en deminutio.

Que es progressio natural en augmentatio

Natural progressio en augmentatio es quant los nombradors acomensan ad 1. Et los denominadors a 2. Et los cascuns dels continua segont natural progressio

que es per addicio de 1. Com son $\frac{1}{2}$, $\frac{2}{3}$, $\frac{3}{4}$, $\frac{4}{5}$4, $\frac{5}{6}$ etc. Et aixi aprop que cascu nombrador o cascun denominador seguent exceras son procha procedent de 1. Et cascu denominador senblantment exeras de 1 son nombrador.

Que es progressio natural en diminutio.

Natural progressio en diminutio es quant totz los nombradors son 1. Et los denominadors acomensan a 2. Et continuant per ajustament de 1, com son 2, 3, 4, 5, 6, 7. Et que los nombradors son uns. Et los denominadors se excerassen de 1. Com son $\frac{3}{4}$, $\frac{3}{5}$, $\frac{3}{6}$, $\frac{3}{7}$ et cetera. Et aixi com los denominadors creyssen segont natural progressio. Et los nombradors diminuessen en valor.

La 2 causa que es de notar deves saber que nos avem nombres rotz prochans et partidas prochanas.

Et sapias que nombres rotz prochans son en la maniera que los nombradors sien nombres prochans. Et senblantment los denominadors. Com son $\frac{5}{8}$ et $\frac{4}{7}$. Et mais propriament non ditz prochans si non del orde de la progressio de la augmentatio como son $\frac{2}{3}$ et $\frac{3}{4}$. Et mot propriament son prochans denotant 1 nombrador com son $\frac{1}{3}$ et $\frac{1}{4}$ ho $\frac{3}{4}$, $\frac{3}{5}$ etc. Et aquestz son del orde de la progressio en diminutio.

Que son partidas prochanas

Partidas prochanas son quant 1 nombre

denominador o 2 nombres prochans com son $\frac{4}{7}$ et $\frac{5}{7}$. Item es de saber que entre 2 nombres prochans non pot esser nombre mejancier mas entre 2 partidas que son prochanas en 1 nombre en 2 senblantz en proporcio que en senblansa de valor poden esser1 & 2 & 3 et 4 & 5. Et tantas unitas mejancieras. Com hom vol. Car qui multiplica lo nombrador et lo denominador del nombre en que son prochanas per qualque nombre en tantas unitas com aura en lo multiplicador sobremonta la major partida la menor en lo nombre de la multiplicatio et per conseguent seran tantas unitas mejancieras como es lo menor nombre prochan del multiplicador.

Regla per creysser o per abreviar la raditz

Item deves saber que totas las radises dels nombres mejanciers que fan plus que lo nombre a la qual monta la multiplicatio de la raditz que es compausada de $\frac{1}{2}$ se deven cercar al comensament per los nombres rotz que an orde en la progressio natural en augmentatio.

Et las radises de aquells que son mendres se deven cercar per aquells que an orde en deminucio.

Et aquo notant en aquells que fan mais, ho deyssendent en aquells que fan mens entro atant que hom vengan als 2 nombres rotz prochans, dels quals la un fay mais & l’autre mens.

Et quant hom los ha atrobas, hom deu pendre aquell que fay mas et multiplicar [lo] lo nombrador et lo denominador per qualque autre nombre, lo qual quant plus grant sera, tant mais valdra et de la multiplicatio del nombrador fer nombrador et aquella del denominador fer denominador.

Per abreviar lo rot.

Aprop hom pot abreviar lo rot en 2 manieras. La premiera es abreviar lo nombrador sustrahent en 1 unitat, et aprop 2, en tant que tant que hom venga a las 2 partidas prochanas que fan mais et mentz. Et qui voldra mais continuar per aver la raditz plus prochana, que torna multiplicar aquella partida que fa mais en son denominador. Et aprop continue la substractio del nombrador com es dit.

La 2 maniera de abreviar lo nombre rot es servar lo nombrador et mudar lo denominador segont l’orde natural de deminutio que se fa ajustant hi 1 aprop 2 et aprop 3, Et continuar entro atant que venga als 2 nombres rotz propdans que fan mais et mentz. Et qui voldra mais continuar que torna multiplicar lo nombre que fa mais. Aprop torne creysser lo denominador com es dit.

Et per aquestas 2 manieras continuant la multiplicatio del nombrador et del denominador ab la substractio del nombrador o ab la mutation del denominador hom pot aver totjorn milhor raditz.

Per trayre la raditz enperfieyta en los nombres rotz

Per aquesta practica meteyssa se tray la raditz enperfieyta dels nombres rotz trasent la raditz del nombrador & del denominador aixi com si eran entiers.

Mas que aprop aquellas 2 radises treitas s redusieyssen manuscrich: redutio a 1 denominador commu. Et de la reductio de la raditz del nombrador hom fan nombrador. Et de aquellas del denominador hom fan denominador et es feyt.

Autras reglas & practicas son ben per cercar aquestas radises enperfieytas. Et en los entiers & en los rotz, las quals layssi car totztemps fan mentz.

Et per aquella desus mesa hom a ensemps radises de las quals la una fa mais et l’autra mens. Com es dit per que hom pot pendre aquell que hom vol.

Per que a mi senbla esser milhor regla et milhor practica que las autras.

Regla et practica special per atrobar alcuns nombres cayratz et cubitz et lurs radises

Et car alcunas vegadas hom vol aver alcuns nombres cayratz o cubitz que ajustant fassan 1 certan nombre. Et per conseguent hom vol aver la raditz d'aquells nombres cayratz o cubitz dels quals nombres se fan questions al quals es mot deficil de respondre aqui non lo sap atrobar.

Et es leugiera causa qui ha la pratica de atrobar los.

Deves saber per saber los atrobar et per trayre lurs radises en la qual ista lo fundament de las respostas yeu ne doni tal regla.

Regla per atrobar aquells cayratz et cubitz

Lo nombre certan que hom vols que aquells nombres cayratz o cubitz ajustatz fassan , hom deu multiplicar per 1 solet nombre dels cayratz o cubitz entro atant que en la multiplicatio se atrobia lo nombre dels cayratz o cubitz. Et quant hom los ha atrobatz, lo nombre que ha atrobat es denominador de en cascun de aquells nombres cayrats o cubitz. Per que la raditz se deu trayre como es istat dit desus en la regla que ensenha de trayre la raditz perfieyta dels nombres rotz.

Per declaratio d'aquesta regla pausi 2 eyxemples. La 1 per los cayratz & l’autra per los cubitz.

Exemple per los cayratz.

Trobi 3 nombres cayratz que ajustatz fassan 13, qui multiplica 13 per 4, que es nombre cayrat, montan 52, en que ha 4 nombres cayratz que son 4, 9 et 3 unitatz. Et yeu non en voli sinon 3. Perque multiplica 13 per l’autre cayrat que es 9 & montan 117, en lo qual nombre ha 3 cayratz que son 100 & 16 & 1. Per so lo premier son $\frac{100}{9}$ que valen 11 et $\frac{1}{9}$, lo segont son $\frac{16}{9}$, que valen 1 et $\frac{7}{9}$, lo tertz es $\frac{1}{9}$. Qui ajustarie aquells 3 nombres cayratz, ells non farian si non 13. Et qui voldra lur raditz que las traga com es istat dit.

Exemple per los cubitz

Troban 3 nombres cubitz que ajustatz

fassan 20. Multiplica 20 per 8,que es nombre cubit, monta 160, en que ha 125 & 27 & 8, que son nombres cubitz et totz son 8^nas. Perque lo premier son $\frac{125}{8}$, que valen 15 et $\frac{5}{8}$, lo segont son $\frac{27}{8}$, que valen 3 et $\frac{3}{8}$, lo tertz son $\frac{8}{8}$ que valen 1. Et aquestz 3 nombres ajustatz fan 20. Et qui voldria la raditz que las traga per la regla de la raditz perfieyta.

Et aquestz exemples abasten per aquestz nombres cayratz & cubitz et per lurs radises.

Per aquestz nombres es de saber que hom pot demandar tal nombre de cayratz ho de cubitz que jamais non se poyrien atrobar per que yeu ho remeti a la discretio d'aquell que lo voldra cercar.

Et aixi es que tot nombre rot ista en 2 causas. So es en redusir, multiplicar et trayre la raditz.

Lo sustrayre et partir.

Et aixi termena & fenis lo nombre rot en la 2^a partida d'aquest compendi en nom de dieu jesus christ al qual sian gratias et lausas. Amen.

Siec se la tersa partida
d'aquest present libre contengut en 4 reglas generals las quals son sufficiens a respondre a totas questions que se poden fer per via de nombre de rasons.

Pueys que sufficcientment dieus ajudant hey tractat dels nombres entiers

et rotz, resta que yeu done & ensenhe per exemples las reglas generals per las quals hom puescan & sapian prestament far sa rason per pendre o donar justament son dreyt, vendent o comprant en totas mercadarias. Et en feyt de companhias hoc et per respondre a questions neccessarias & hutils et delectablas al entendement del home.

Et per aysso complir, 4 reglas per orde pausarey, de las quals darey diverses exemples, segont que en diversas manieras poden ajudar & servir.

La 1^a se appella regla de 3. Et la 2 se appella regla de falsa positio. La 3 se appella de 2 falsas positions. La 4 se appella regla de appositio & remotio.

Et d'aquestas 4 reglas tractarey per orde.

Et premierament de la regla de 3, per la qual se fan totas rasons comunas que se poden fer en mercadarie.

La qual a 3 partidas per rason de temps o de mesura o de pes ab lo gasanh, o pretz, et per rason de autras causas diversas.

Et appella se regla de 3. Car totztemps hi a 3 causas, 2 senblantz et 1^na desenblant. Et si plus ni avia se redusieyssen en aquellas 3.

Et podes cognoysser quant sera de la premiera partida quant no hi a sinon 1 desenblant.

De la 2^a quant hi a 2 desenblans.

Et de la 3^a quant hi a 3 desenblans et se perpausan en tal maniera.

La premiera

Multiplicant so que voles saber per son contrari. Et aprop partir lo per son semblant.

La segonda

Multiplica la causa que sabes per la causa que li es de tot desenblant. Et aprop partis ho per son senblant.

La tersa

Multiplica lo gasanh o la valor o la moneda o autra causa que vulhas saber per la multiplicatio de las 2 causas mais deyssanblans que tu sabes, aprop parteys per las multiplications de las causa que restan.

Per aquestas 3 reglas es de saber que totztemps que hom atrobian temps o mesura o pes ab argent, que hom deu multiplicar l’argent per son temps o per sa mesura o per son pes, & quant hi a 2 temps o 2 mesuras o 2 peses, lo es de la premiera partida de la regla.

Et quant ni hi a si non 1 temps ab son gasanh o 1 mesura ab sa valor o 1 pes ab son pretz, lo es de la

2 partida de la regla. Et quant non hi a mas 1 temps o 2 gasanhs ho 1^a mesura o 2 valors ho 1 pes o 2 pretz, lo es [es] de la 3 partida de la regla.

Et deves be notar que lo partidor tostemps respon de son contrari e non jamais de son semblant si non en las rasons del aut que se fan per lur regla.

Item mais es de notar que per aquellas 4 reglas generals sobre dictas se fan totz los partimentz engoals.

Et garda la regla de 3, es plus necessaria en mercadaria et plus la premiera partida. Et per so d'aquella parlarey, aplicant la en feit de monedas & de mesuras de pes et en feyt de conpanhia. Et premierament pausarey los exemples generals que se poden aplicar a totas mercadarias.

Sieguen se los exemples generals de la regla de 3 sens temps, mesura et pes que se poden applicar a totas mercadarías.

Et premierament yeu demandi si quant val tant, per exemple, si 4 valen 7, que valen 12. Multiplica 12 que voles saber per 7, que es son contrari, montas 4per 4 que es son senblant, que ne venen 21 et aytant valen.

Item 4 $\frac{1}{2}$ valen 7, que valen 13. Resposta: multiplica 13 per 7, que es son contrari, montan 91 que deves partir per 4 $\frac{1}{2}$ mas premierament redusis ton partidor et la summa que deves partir a un denominador, monta lo partidor 9. Et la summa que deves partir 182,182 per 9, que ne venen 20 & $\frac{2}{9}$ & aytant valen. Item 4 $\frac{1}{2}$ valen 7 $\frac{2}{3}$, que valen 13. Resposta: multiplica 13 que voles saber per 7 $\frac{2}{3}$ que es son contrari, et digas premierament 3 vegadas 7 son 21, & 2 fan 23. Aras multiplica 13 per 23, montan 299, que deves partir par 4 $\frac{1}{2}$, que montan $\frac{9}{2}$ et deves ho redusir en aquesta maniera: deves multiplicar 9 per 3 et 2 par 299, aixi com es pausada aysi la figura sus lo marge, redusis o tot monta lo partidor 27 & la summa que se deu partir monta 598. Parteis 598 par 27, que ne ve 22 & $\frac{4}{27}$ et tant valen.

Item 4 $\frac{1}{2}$ valen 7 $\frac{2}{3}$, que valen 13 $\frac{3}{4}$. Resposta: multiplica 13 $\frac{3}{4}$ que voles saber per 7 $\frac{2}{3}$ que es son contrari, e redusis premierament los entiers ab sos rotz et premierament lo contrari de so que voles saber et digas: 3 vegadas 7 son 21, & 2 son $\frac{23}{3}$. Item multiplica aprop so que voles saber & digas

4 vegades 13 son 52, et 3 fan 55. Aras multiplica 55 per 23, montan $\frac{1265}{12}$ que deves partir per 4 $\frac{1}{2}$ que son $\frac{9}{2}$. Redusis o en aquesta maniera: multiplica 9 par 12 et 2 par 1265, en aquesta maniera seguent aixi com appar aissi al marge. Et redusis monta lo partidor 108. Et la summa que se deu partir monta 2530. Aras partis 2530 par 108, que ne ve 23 & $\frac{46}{108}$. Et aitant valen.

Item si la $\frac{1}{2}$ et $\frac{1}{3}$ de una causa valen 3, quant val tota la causa. Resposta: redusis $\frac{1}{2}$ et lo $\frac{1}{3}$, que son $\frac{5}{6}$, forma ta questio: si 5, que son $\frac{1}{2}$ et $\frac{1}{3}$ de 6 valen 3, que valen 6 que son tota la causa entiera. Multiplica 6 que voles saber par 3 que es son contrari, monta 18. Parteis per 5, que ne ve 3 et $\frac{3}{5}$ et aytant val tota la causa, et es feyt lo conte.

Item si lo $\frac{1}{3}$ & lo $\frac{1}{4}$ de 1^a causa valen 3, que val lo sobre plus. Resposta: redusis $\frac{1}{3}$ et $\frac{1}{4}$ que son $\frac{7}{12}$. De 7 entro a 12, ha 5. Digas si 7 valen 3, que valdran 5. Multiplica 5 que voles saber per 3 que es son contrari, montan 15,per 7 que ne ve 2 et $\frac{1}{7}$. Et aytant val lo sobre plus.

Sieguen se los eyxemples generals pausas a las causas particulars et premierament en monedas.

Premierament si 4 escuts valen 7 motons, quant valen 12 escuts. Resposta: multiplica 12 escuts per 7 motons, que es son contrari, montan 84, que partey par 4 escuts que es son senblant, que ne ve 21, et 21 moton[s] valen los 12 escuts quant los 4 valen 7.

Item 4 escuts $\frac{1}{2}$ valen 9 motons, quant valen los 13. Resposta: multiplica 13 escuts que voles saber per 9 motons, que es son contrari*, que montan 117 par 4 escuts et $\frac{1}{2}$ que es son se[n]blant, & car lo partidor Ha nombre rot, redusis ho tot a un senblant. Et premierament digas 2 vegadas 4 so 8, et 1, son $\frac{9}{2}$ que sera lo partidor. Et car lo partidor es $\frac{1}{2}$ et la summa que se deu partir es 117 entiers, digas 2 vegadas 117 fan 234,doncas 234 par 9, que ne ve 26 et aytant valen. Item si 4 escuts $\frac{1}{2}$ valen 7 motons $\frac{2}{3}$ que valen los 13

escuts. Resposta: multiplica 13 escuts per 7 motos & $\frac{2}{3}$, que es son contrari, et digas premierament 3 vegadas 7 son 21 & 2 fan 23, aras multiplica 13 per 23, es $\frac{299}{3}$. Deves par[tir] par 4 & $\frac{1}{2}$, que montan $\frac{9}{2}$, consi ton partidor que es 3, lo qual 3 al dire $\frac{299}{23}$ & los 3 es lo partidor multiplicat en aquesta maniera tot a un senblant monta lo partidor 27 & la summa que se deu partir es 598. Parteis doncs 598 par 27, que ne ve 22 & $\frac{4}{27}$ et aitant valen los 13 escuts quant los 4 $\frac{1}{2}$ valen 7 et $\frac{2}{3}$.

Item si 4 escuts $\frac{2}{3}$ valen 7 motons $\frac{2}{3}$, quant valen [los 13] escuts $\frac{3}{4}$. Resposta: multiplica 13 escuts $\frac{3}{4}$ que voles saber per 7 motons $\frac{2}{3}$, que es son contrari, et premierament redusis los entier[s] ab lurs rotz. Et premierament lo contrari de so que voles saber, et digas 3 vegadas 7 son 21 & 2 fan 23. Item mais so que voles saber et digas 4 vegadas 13 son 52, et 3 fan 55. Aras multiplica 55 par 23, montan $\frac{265}{12}$ que deves partir per 4 escuts $\frac{1}{2}$ que son $\frac{9}{2}$. Redusir en aquesta maniera monta lo partidor 108,et la summa que deves partir 2530. Aras530 par 108, que ne ve 23 et $\frac{46}{108}$. Et 23 motons et $\frac{46}{108}$ de moto valen los 13 escuts $\frac{3}{4}$.

Item si $\frac{1}{2}$ valia $\frac{2}{3}$ de moto quant valdran los

$\frac{3}{5}$ de escut. Resposta: multiplica $\frac{3}{5}$ de escut que voles saber per $\frac{2}{3}$ de moto que es son contrari, monta la multiplicatio $\frac{\mathrm{\S }}{15}$ que deves partir par $\frac{1}{2}$ de escut que es son senblant, mas premierament redusis, monta lo partidor 15 et la summa que se deu partir, monta 12, aras partis 12 par 15, que ne ve $\frac{12}{15}$. Et aytant valen.

Nota las 3 rasons seguens per retornar 1^a moneda en autra.

Un home deu en 1^a botiga 13 doblas del temps que lo moto valia 22 doblas. Demandi quant deu pagar d'aquellas 13 doblas de present quant lo moto non val mas 19. Resposta: digas si las 22 doblas d'aquell temps non valien si non 19 d'aquest temps, quant valen los 13 d'aquell temps. Multiplica 13 que voles saber par 19 que es son contrari, monta 247,par 22, que ne ve 11 et $\frac{5}{22}$. Et 11 doblas & $\frac{5}{22}$ de dobla deu pagar per aquellas 13 et es feyt lo conte.

Item un home deu a 1 autre 13 escuts et vol lo pagar en motons. Et l’escut val 13 doblas et lo moton 19 [doblas]. Demandi quantz motons li deu bayllar per aquells 13 escuts. Resposta: multiplica los 13 escuts par la valor de 1 escut

monta 416 [doblas]. Parteis par la valor de 1 moton, so es per 19, que ne ve 21 & $\frac{17}{19}$. Que valen 17 doblas et 21 moton[s] & 17 doblas li deu bayllar per los 13 escuts.

Et semblantment fera qui vol metre motons en escuts que hom deven multiplicar los motons per lor valor & partir la multiplicatio per la valor del escut.

Item un home de avinho deu a 1 home [de] montpellier 13 liuras de moneda d’avinho. Demandi quantas liuras deu donar de la moneda de montpellier dela et desa, contant liuras per 20 souses et lo sou per 12 deniers. nota aquesta _☞
regla Resposta: en talas questions, tu deves saber moneda mejansciera de la qual tu sabes la valor de cada una de la[s] monedas. Et per aquella mejansarie tu deves far ta rason.

Per eyssemple, en la questio feyta tu sabes o deves saber que la dobla a montpellier val 19 deniers, et en avinho val 16 deniers.

Et aixi las 10 liuras de montpellier valen 16 liuras d’avinho et las 5 valen 8. Digas doncas : si 8 liuras d’avinho valen 5 de montpellier, que valen las 13 d’avinho. Multiplica las 13 liuras d’avinho que voles saber per 5 de montpellier que es son contrari, montan 65,par 8 liuras d’avinho que es son senblant que ne ve 8 liuras & $\frac{1}{8}$. Et 8 liuras et $\frac{1}{8}$ de liuras li deu bayllar de la moneda de montpellier per las 13 d’avinho & es feyt.

Per saber fer lo sou de fi de una moneda o de diversas de las quals hom sap a quant son de fi o de ley.

Per fer lo sou de fi, premierament es mestier de saber que en lo marc ha 8 onsas et en la onsa ha 24 deniers et en lo denier ha 24 gras. Et lo gra se met en $\frac{8}{9}$ o en 24 peletz, et aixi tot jorn diminuent per 24. Nota.

Item mais deves saber que 1 march de pes d’argent si es a 12 deniers de ley et aixi 12 deniers de ley valen 1 march de pes et 1 denier de ley val gras 16 deniers de pes. Et $\frac{1}{8}$ de gra de ley val 2 gra de pes.

Eyxemple: yeu demandi 7 marchs 4 onsas 9 deniers tot de pes, ha 5 deniers et 10 gras ley, quant an de fi? Resposta: per la regla de 3, tu deves metre 1 march et lo fi et so que voles saber lo cascu per fi en sa mendre valor que se sie perpausada, et multiplicar la summa que voles saber par la summa del fi. Et so que vendra partir per summa de 1 march et so que ne vendra par lo partir sera senblant a la summa mendre perpausada per que ella se deu redusir en las mais valens partent per 24 o per 12 si eran deniers et per cada sou contar 1 march.

Eyxemple en lo cas prepausat, la mendre summa prepausada en lo fi son gras, perque met 1 march

1 marc = 8 × 24 × 24 = 4608 gras en gras, monta 4608, que sera ton partidor. Aprop met los 5 deniers de fi en gras, montan 120 et 10 que ni avia es lo fi: 130 gras. Item mais, met los 7 marcx 4 onsas 9 deniers tot 4608(7 + $\frac{4}{8}$ + $\frac{9}{\mathrm{8\; \times \; 24}}$) = 4608(7+ $\frac{1}{2}$ + $\frac{3}{64}$) = 4608(7 + $\frac{35}{64}$) = 4608( $\frac{\mathrm{7\; \times \; 64\; +\; 35}}{64}$) = 72 × 483 = 34776 en gras, montan 34776 que deves multiplicar per 130, la multiplicatio: 4520880 gras, par 4608, que ne ve 981 & $\frac{432}{4608}$, los gras entiers met en deniers partent los par 24 que ne venen 40 deniers et restan 21 gras. Item los 40 deniers met en souses partent par 12, ne venen 3 et restan 4 deniers; montan doncas 7 marcx las 4 onsas & 9 deniers de pes, 3 souses que son 3 marcx 4 deniers 21 gra[s] et $\frac{432}{4608}$, lo qual nombre rot si lo abrevias ve a $\frac{3}{32}$. Et aixi as lo fi que volias aver et lo sobre plus es autre metalh.

Autra practica plus presta.

Per autra practica plus breva assaber lo sol de fi sobre dit dona reglas que s'en sieguen.

Per onsas.

Per cada denier que ha lo march de ley la onsa ha 3 gras, per cada gra que lo march de la onsa ha $\frac{1}{8}$ de gra.

Per deniers.

Per cada denier que ha lo march de ley lo denier ha $\frac{1}{8}$ de gra et per cada gra que ha lo march de ley, lo denier ha $\frac{1}{192}$ de gra.

Per gras.

Per cada denier que lo march ha de ley lo gra ha $\frac{1}{192}$ de gra e per cada gra que lo march ha de ley, lo gra ha $\frac{1}{460}$ de gra.

Per saber fer mesclas de bilho per metre lo al fi en la maniera que lo vulhan

Per saber fer mesclas premierament es de saber que totztemps 12 deniers mescla sie argent o metalh fan 1 march de pes et per so hom pot prestament saber quant ha de fi et quant ha de coyre en 1 march. Car si disem que sie a 7 deniers lo hi a 7 deniers de fi & 5 de coyre que restavan acomplir 12 deniers que fan lo march. Et per saber fer venir al fi metent ho levant lo son 2 reglas.

La premiera regla.

Saubut que hom ajan lo fin de tot per lo nom de fi de un marc de non saber lo non fi de tot, per metre o per levar.

Aquesta regla es de saber que quant la regla ditz que per lo non fi deu hom saber lo fi de tot.

Vol dire que hom deu multiplicar lo tot non fi per lo fi de 1 march. Et aprop partir per lo non fi de1 march. Et senblantment per lo fi de 1 march so es que hom deu multiplicar tot lo fi per lo non fi de un march. Et la vegada metre o levar so que sera necessari. Et aixi aprop que la regla non dona sinon lo partidor.

Eyxemple

Un home ha 10 marchx de coyre que vol metre a 7 deniers de ley, demanda quant li fa mestier de argent fi per los hi

fer venir. Resposta: diga de 7 deniers de ley a 12, ha 5 de coyre, digas per la regla de 3: si 5 deniers de coyre me donan 7 d’argent fi, quant me daran 120 deniers de coyre que son los 10 marcx, multiplica per 7, monta 840,per 5, que venen 168 deniers d’argent, et 168 deniers d’argent fan mestier a metre los 10 marcx de coyre a 7 deniers de ley.

Item un merchant haja 10 marcx d’argent, si los quals vol metre en bilho que sie a 7 deniers de ley, demandi quant ha mestier de coyre per fer los hi venir. Resposta: per la regla de 3, digas si 7 deniers de fi me dona 5 deniers de de coyre, quant me daran 120, que fan los 10 marcx. Multiplica per 5, monta 600,per 7, que ne ve 95 & $\frac{5}{7}$, et 95 deniers de coyre & li fan mestier per redusir los 10 marcx a 7 deniers de ley et es feyt.

Item un home ha 10 marcx de bilho a 7 deniers de ley los quals vol melhorar et fer venir a 8. Demandi quant hi deu metre d’argent fi per fer los hi venir. Resposta per la regla de 3. Sapias quant hi a de fi et quant de coyre. Lo hi a 70 deniers de fi et 50 de coyre. Aras podes veser que de 8 en que vol metre son bilho entro 12 ha 4. Digas si 4 me donan 8, quant me daran 50, multiplica 50 per 8, monta

400,per 4, que ne venen 100, delsquals leva 70, que avias davant, restan 30 et 3[0] deniers d’argent fi li fay mestier, metre en aquells 10 marcx per fer los venir a 8 deniers de ley et es feyt.

Item 1 merchant ha 10 marcx de bilho a 7 deniers los quals vo pejurar et tornar los a 6 deniers de ley. Demandi quant li fa mestier de coyre per fer los hi tornar. Resposta per la regla de 3: sapias quant hi a de fi et quant de coyre. Lo hi a 7 deniers de fi et 5 deniers de coyre. Aras podes veser que de 6, en que 2 vol redusir son bilho, entro 12, a 6. Digas: si 6 de fi me donan 6 de coyre, quant me daran 70 que yeu hey a multiplicar 70 per 6, monta 70 × 6 = 420 ÷ 6 = 70 400,per 6 de fi, ne ve 70, dels quals leva ne 20 que avias, resta 50 et 50 deniers de coyre fan mestier a metre en los 10 marcx per fer los retornar a 6 de ley et es feyt.

Item 1 ha 10 marcx de bilho que es a 7 deniers de ley, los quals vol melhorar & redusir a 8. Demandi quant deu levar del coyre que hi es per fer los venir. Resposta per la regla de 3. Sapias quant hi a de fi & quant de coyre. Lo hi a 70 deniers de fi* * 50 de coyre aras podes veser que de 8 de fi entro a 12 ne a 4 de coyre. Et per so digas si 8 me donan 4, que me daran 70. Multiplica

70 per 4 montant 280, partes per 8, que ne ve 35 et 35 deniers de coyre deu levar de 50 et restan 15, que deu levar d'aquells 10 marcx que son a 7, per far los retornar que sien a 8 deniers de ley.

Item 1 merchant ha 10 marcx de bilho a 7 deniers de ley los quals vol pejurar et far venir a 6 deniers de ley. Demandi quant deu levar de l’argent fi per fer las hi tornar. Resposta per la regla de 3. Sapias quant hi a de fi et quant de coyre. Lo hi a 70 deniers de fi et [50] de coyre. Aras podes veser que los 50 deniers de coyre valen 6 deniers de fi. Per so digas 6 de coyre me donan 6 deniers de fi, quant me daran lo 50 deniers de coyre? Multiplica 50 per 6 deniers de fi, monta 300, partis per 6 manuscrich: 6 deniers de coyre que ne ve 50, los quals leva de 70, restan 20 et 20 deniers de fi deu levar d'aquells 10 marcx per fer los retorna a 6 deniers de ley & es feyt.

La 2^a regla del bilho.

Del defalhiment del mendre al mejancier fay nombrador & del sobreplus del major al mejancier fay denominador del menor per saber applicar aquesta regla a la regla de 3. Et deves saber que quant tu voldras saber quant te hi fa mestier del major tu hi deves dire, si tant que es denominador me dona tant, que es nombrador quant me dara tant que es tot lo nombre que vol saber. Et per lo contrari quant voldras

saber quant te fa mestier del mestre , digas: si tant que es nombrador me dona tant que es lo denominador, quant me dara tant que es lo major que vols saber.

Exemple

Un home ha 10 marcx de bilho que es a 4 deniers et vol lo melhorar et far lo venir a 5 deniers de ley. Demandi quant li fay mestier metre de bilho que es a 7 deniers de ley. Resposta: 4 es mendre que 5 de 1, et 7 es major que 5 de 2, que deves mestre en ta maniera $\frac{1}{2}$. Aras digas per la regla de 3: si 2 me donan 1, quant me daran 10 que voli saber? Multiplica 10 per 1, monta 10, partis per 2 que ne ve 5, et 5 marcx de bilho de 7 deniers fan mestier per mestre los 10 marcx que son a 4 deniers, a 5. Et aurey 15 marcx que son a 5 deniers de ley, et cetera.

Item 1 merchant ha 10 marcx de bilho que es a 8 deniers de ley, la qual vol pejurar et metre a 5 deniers de ley. Demandi quant hi deu metre de bilho que es a 3 deniers de ley. Resposta: 3 es mendre que 5 de 2, et 8 es major que 5 de 3. Escriu los en tal maniera $\frac{2}{3}$. Aras digas si 2 me donan 3, quant me daran 10? Multiplica 10 per 3, monta 30, partis per 2, que ne ve 15, et 15 marcx de bilho que es a 3 deniers fan mestier per mestre a 5, ad aquells 10 marcx que son

a 8 et aura hi 25 marcx de bilho que seran a 5 deniers de ley.

La regla per saber lo fi et lo non fi del aur es aquesta.

Per saber lo fi o lo non fi del aur la regla es aquesta. Quant tu auras un pes d’aur en que ha mescla. Et voles saber quant hi a d’aur, si multiplica lo nombre del pes que pesa per lo nombre dels cayratz a que es. Et apropper 24 et auras lo fi del aur segont lo pes que as multiplicat.

Car si as multiplicat marcx tu auras marcx. Et si as multiplicat onsas tu auras onsas.

Et quant tu auras 1 pes d’aur fi & voles hi fer mescla multiplica aquell pes d’aur fi per 24. Aproplo per los cayratz en lo qual voles metre ton aur et saubras quant pesa tot l’aur quant sera feyta la mescla pes per pes como es dit desus, del qual pes leva ne lo pes del aur fi. Car so que restara sera lo non fi que hi fey mestier.

Exemple: 1 canbiador avia de aur 12 onsas a 16 cayratz et vol lo porgar et far venir a 24 cayratz. Demandi quant hi aura d’aur fi. Resposta: multiplica 12 onsas que ell ha per 18 cayratz que montan 192, per 24, que ne ve 8. Et 8 onsas d’aur fi atrobara quant sera istat porgat.

Item 1 canbiador avia aur a 15 cayratz et fer los porgar & venir a 24 cayratz & atroba que ell ha 9 onsas d’aur fi. Demandi quant pesava tot per saber quant hi avia de non fi. 9 onças d'aur a 24 carats = 9 × $\frac{24}{15}$ d'onças d'aur a 15 carats. I avia donca 14 e $\frac{2}{5}$ d'onças a la debuta. Coma resta 9 onças de fin, i avia (14 + $\frac{2}{5}$) - 9 = 5 + $\frac{2}{5}$ de non fin Resposta: multiplica 24 per 9 onsas, monta 216,per 15 que ne ve 14 et $\frac{6}{15}$, que valen $\frac{2}{5}$, 14 et $\frac{2}{5}$ de onsa pesaria per que lo hi avia 5 onsas e $\frac{2}{5}$ de onsas de mescla & deves saber per aquestas rasons que lo plus fi aur que sie es a 24 cayratz per que si non hi es lo hi a mescla.

Siec se la applicatio dels eyxemples generals sobre meses en feyt de draparia que es per applicar en la regla en feyt de mesuras.

Una pessa de drap que tira 11 cannas costa 9 motons, que costan 3 cannas. Resposta: multiplica 3 que voles saber per 9 que es son contrari, monta 27, partis per 11 que es son senblant, que ne ve 2 motons & $\frac{5}{11}$ et tant costarian las 3 cannas.

* cannas Item 1 pessa de drap que tira 11* et $\frac{1}{2}$ costa 9 motons, que costaran las 5 cannas. Resposta que voles saber multiplica 9 per 5, montan 45, partis per 11 et $\frac{1}{2}$. Et car en lo partidor ha nombre rot, redusis ho tot ad 1 senblant en aquesta maniera. Premierament

digas 2 vegadas 11 son 22, et 1 fan $\frac{23}{2}$, que seran ton partidor. Et car lo partidor es $\frac{23}{2}$ et la summa que se deu partir es 45 entiers, digas 2 vegades 45 fan $\frac{90}{2}$, partis 90 per 23 que ne ve 3 et $\frac{21}{23}$. En totas las rasons seguens avisa del nombre rot en lo multiplicar § & en lo partir

Item 11 cannas $\frac{1}{2}$, costan 9 & $\frac{2}{3}$ que costaran 5 cannas. Resposta: multiplica 5 per lo $\frac{2}{3}$ et premierament digas 3 vegadas 9 et 2 son 29, aras multiplica 5 per 29, fan 145, que son $\frac{145}{3}$, que deves partir per 11 et $\frac{1}{2}$, que montan $\frac{23}{2}$, redusis, monta lo partidor 69, et la summa que se deu partir 290, partis 290 per 69, ne ve 4 et $\frac{14}{69}$, et tant costan las 5 cannas.

Item 3 cannas & $\frac{1}{2}$ costan 5 ? et $\frac{2}{3}$, que costan 5 cannas et $\frac{3}{4}$. Resposta: multiplica 7 et $\frac{3}{4}$ que voles saber per 5 et $\frac{2}{3}$ que es son contrari. Et redusis premierament los entiers ab lurs rotz et premierament lo contrari de so que voles saber et digas 3 * legir: $\frac{17}{3}$ vegadas 5 son 15, et 2 fan 17* Item aprop son de senblant et so que voles saber et digas 4 vegadas 7 son 28, et 3, fan $\frac{31}{4}$, aras multiplica 31 per 17, montan 527, que deves partir per 3 & $\frac{1}{2}$, que fan $\frac{7}{2}$. Redusis, monta lo partidor 84, et la summa que deves

partir monta 1054, aras partis 1054 per 84, que ne ve 12 et $\frac{46}{84}$ et 12 motons et $\frac{46}{84}$ costarian las 7 cannas et $\frac{3}{4}$.

Item 1^a pessa de drap tira 11 cannas et 5 palms e $\frac{1}{2}$. Costa 7 motons, que costan 3 cannas. Resposta: per so que tu as palms deves metre tota la pessa en palms que son 93 et $\frac{1}{2}$. Item plus las 3 cannas que voles saber montan 24 pa[l]ms, aras podes fer ta questio disens: si 93 pa[l]ms et $\frac{1}{2}$ costan 7 motons, que costaran 24 palms. Resposta: multiplica 24 que voles saber per 9 que es son contrari, montan 161, partis per 93 et $\frac{1}{2}$, et premierament redusis, monta lo partidor 187 et la summa que se deu partir monta 432, partis 432 per 187 que ne ve 2 et $\frac{58}{187}$, et aitant costarian las 3 cannas.

Senblantment fay si de la part que tu voles avia pa[l]ms et de cada part avisant te del nombre rot. Aixi com $\frac{2}{3}$ de una canna de drap costaria $\frac{3}{4}$ de flori, que costarian los $\frac{2}{5}$. Resposta: multiplica los $\frac{2}{5}$ per $\frac{3}{4}$, montan $\frac{6}{20}$, que deves partir per $\frac{2}{3}$, redusis, monta lo partidor 40 et la summa que deves partir 18, partis donc 18 per 40, ne ve $\frac{18}{40}$, et aitant valen lo $\frac{2}{5}$.

Item la $\frac{1}{2}$ et $\frac{1}{3}$ de 1^a canna de drap val 3 floris, que val tota la canna. Resposta: redusis $\frac{1}{2}$ et lo $\frac{1}{3}$, son $\frac{5}{6}$, forma ta questio: si 5 valen 3 que valen 6, multiplica 6 que es la causa entiera que vales saber per 3, que es son contrari, monta 18, que deves partir per 5 que es son senblant, que ne ve 3 et $\frac{3}{5}$, et aytant costaria tota la canna.

Item si la $\frac{1}{3}$ et la $\frac{1}{4}$ de 1^a canna val 3 floris, que valdra lo sobreplus. Resposta: redusis $\frac{1}{3}$ et $\frac{1}{4}$, son $\frac{7}{12}$, de 7 entro a 12 a 5, et digas si 7 valen 3 floris que valen 5, multiplica 5 que voles saber per 3, montan 15, partis 15 per 7, ne ven 2 et $\frac{1}{7}$ et aitant costara lo sobre plus de $\frac{1}{3}$ et $\frac{1}{4}$ de 1^a canna de drap.

Item yeu hey 2 cannas de drap que han d’ample 7 pams et voldria la forrar de autra drap que ha 5 pams d’ample. Demandi quant m’en farie mestier d’aquell de 5 a complir aquell de 7. Resposta: en tals questions tu deves saber quantz pams cayratz ha en lo drap que tu voles forrar. Aprop deves saber quantz pams cayratz en lo drap so es en 1^a canna d'aquell de que voles fer la forradura. Aproplos pams cayratz que tu voles forrar per aquells de que voles fer la forradura, Et so que ne vendra seran las cannas que te fan mestier.

Et sapias que per saber los pams cayratz e 1^a causa plana que totztemps tu deves multiplicar la longuesa per la larguesa et so que ne vendra fan los pams cayratz.

Eyxemple en la questio desus multiplica la longuesa per la larguesa de 2 cannas que son 16 pams per la larguesa que es 7 pams, monta 112 pams cayratz.

Aprop multiplica 1^a canna que es 8 pams lonc per 5 que ha d’ample, monta 40 pams cayratz que fan 1^a canna, digas aras si 40 me venen de 1^a canna, de quant me vendran 112.

Resposta: multiplica 112 per 1, fan 112,per 40, ne venen 2 et $\frac{32}{40}$, lo qual nombre rot si lo abrevias per 8, ne ve de segur $\frac{4}{5}$.

Et si voles saber que valen de longuesa aquells $\frac{4}{5}$, multiplica lo nombrador que es 4 per los pams de 1^a canna que son 8, monta 32,per 5, ne ve 6 et $\frac{2}{5}$, auries doncas del mendre drap 2 cannas 6 pams et $\frac{2}{5}$ de palm et es feyt.

Item  yeu hey 2 cannas & $\frac{1}{2}$ de drap que ha de larc 3 pams & $\frac{3}{\mathrm{5\; 4}}$ et voli lo forrar de 1 autre drap que ha de larc 5 pams & $\frac{2}{3}$. Demandi quantas cannas me son neccessarias del drap de 5 pams et $\frac{2}{3}$ per forrar aquell de 3 [pams] et $\frac{1}{4}$. Resposta: quantz pams cayratz fan las 2 cannas et $\frac{1}{2}$. como es dit en la rason desus

et multiplica 2 cannas et $\frac{1}{2}$ per la longuesa que es 3 pams. Aprop so que ne vendra per la larguesa que es 3 pams et $\frac{1}{4}$, monta tot $\frac{520}{8}$, met los entiers, fan 65, et 65 pams cayratz ha en lo drap que voles forrar. Item sapias quantz pams cayratz ha en 1 canna del drap que ha de larc 5 pams & $\frac{2}{3}$ et digas 8 vegadas 5 et $\frac{2}{3}$, montan 45 et $\frac{1}{3}$, aras fay ta raso: si 45 et $\frac{1}{3}$ me son vengutz de 1, de quant me vendran 65. Multiplica 65 per 1, fan 65,per 45 et $\frac{1}{3}$, ne ve 1 et $\frac{59}{136}$, et per so podes veser que 1 canna et $\frac{59}{136}$ te fan mestier del drap que ha 5 [pams] et $\frac{2}{3}$ a complir aquell que ha 3 pams et $\frac{1}{4}$.

Prova per aquestas 2 questions.

Item quant hom vol provar si lo conte es ben feyt en senblantz questions com son las derrierament feytas, hom deu multiplicar las mesuras atrobadas per sa longuesa. Et aprop so que ne vendra per la larguesa et si d'aquellas multiplications fan tanttost tantz cayratz com fa la causa de la qual hom an volgut atrobar, sa engala rason la vegada es bona. Et si non si atroba ella es mal feyta.

Eyxemple en la rason premiera desus feyta es trobar que acomplir 2 cannas que an de larc 7 pams fan mestier 2 cannas & $\frac{4}{5}$. Multiplica 2 cannas & $\frac{4}{5}$

per la longuesa que es 8 pams & per la larguesa que es 5 pams per veser la multiplicatio fara 112 pams cayratz com fan las 2 cannas que an de larc 7 pams.

Siec la applicatio dels eyxemples sobre pausas en feyt de telas

Per applicar la regla de 3 al feyt de las telas es assaber que tota las rasons senblans que son istadas feytas de drap se poden fer en telas. Car tot es un.

Eyxemple: 1 corda de tela tira 11 cannas costa 5 motos, que costan las 3 cannas. Resposta: multiplica 3 cannas per 5 motos, montan 15, per 11 que ne ve 1 & $\frac{4}{11}$ & aytant valen .

Item 1 corda de tela que tira 11 cannas et $\frac{3}{4}$ costa 5 floris & $\frac{1}{2}$, que costan 3 cannas & $\frac{1}{3}$. Resposta: multiplica cannas & $\frac{1}{3}$ per 5 floris & $\frac{1}{2}$. Et premierament met los entiers ab sos rotz et digas en so que voles saber 3 vegadas 3 fan 9 et 1 son $\frac{10}{3}$. Item per son contrari digas 2 vegadas 5 fan 10 & 1 son 11. Aras multiplica 10 per 11, monta $\frac{110}{6}$ que deves partir per 11 ' $\frac{3}{4}$. Et premierament digas 4 vegadas 11 son 44 et 3 fan $\frac{47}{4}$. Redusis ho tot ha un senblant, monta lo partidor 282  et la summa que se deu partir es 440,

manuscrich: 2 doncas 440 per 282 que ne ve 1 & $\frac{1148}{282}$ lo qual nombre rot si lo abrevias per mitat torna en $\frac{579}{141}$ et tant valen las 3 cannas et $\frac{1}{3}$.

Item 1^a © cannas et $\frac{3}{4}$ costa 5 floris et $\frac{2}{3}$; que costaran las 5 aunas & 3 pams $\frac{1}{2}$. Resposta: multiplica las 5 aunas & 3 pams et $\frac{1}{2}$ que voles saber per 5 floris et $\frac{2}{3}$ que es son contrari. Et premierament fay de la[s] 5 aunas, pams et valha cascuna auna 5 pams, montan 25 & 3 pams et son 28 $\frac{1}{2}$. Item totz aquells pams redusis los en $\frac{1}{2}$ et fan ab lo $\frac{1}{2}$ $\frac{57}{2}$. Aprop redusis los 5 floris en terces, fan 15 et 2 et son $\frac{17}{3}$. Aras multiplica so que voles saber so es 17 per 57 montan $\frac{969}{6}$ que deves partir per 11 aunas & $\frac{3}{4}$. Premierament redusis totas las aunas en $\frac{1}{4}$ de palm. Et digas 4 vegadas 11 fan 44 et 3 fan 47 d'auna. Item 5 vegades 47 per fer quartz de palm montan $\frac{235}{4}$. Aras redusis ton partidor & la summa que deves partir a un senblant, monta lo partidor 1410 et la summa que deves partir 3876,doncx 3876 per 1410 que ne ve 2 et $\frac{1056}{1410}$ lo qual nombre rot si lo abrevias torna a $\frac{176}{235}$. Valen doncas las 5 aunas & 3 pams & $\frac{1}{2}$, 2 floris

et $\frac{176}{235}$, et es feyt.

manuscrich: 397 Item demandi 379 aunas de tela, quantas cordas fan? la corda ha 11 aunas et $\frac{3}{4}$. Resposta: digas per la regla de 3: si 11 aunas $\frac{3}{4}$ valen 1, que valen 379? Multiplica 379 per 1 montan 379, per 11 $\frac{3}{4}$, mas premierament redusis los entiers del partidor ab sos rotz, montan $\frac{47}{4}$, aprop redusis la summa que deves [partir] al senblant del partidor et digas 4 vegadas 379 son 1516,doncx 1516 per 47 que ne venen 32 et restan 12, que son $\frac{12}{4}$ de auna que valen 3 aunas. Valen doncas aquellas 379 aunas 32 cordas et 3 aunas & es feyt.

Per aquestz eyssemples feytz de draps & de telas se entenden de fer totz los eyxemples & totas las rasons que se poden fer en feyt de mesuras.

Siec se la multiplicatio dels eyxemples generals de la premiera partida regla de 3 en feyt de pes.

Per fer las rasons que se fan per la premiera partida de la regla de 3, simpla es de saber que generalment se pausan como aquellas de las monedas & de mesuras disent.

Per eyxemple:

Si 1 liura de pes valen 5 gros, que valen 7 liuras. Resposta: multiplica 7 que voles saber per 5 que es son contrari, montan 35,per 3, ne ve 11 et $\frac{2}{3}$ & tant valen.

Item 1^a carga d’aver costa 23, que costan las 13. Resposta: multiplica 13 que voles saber per 23 que es son contrari, monta 299, partis per 300 que fa la carga, ne ve $\frac{299}{300}$ & tant valen.

Item 7 liuras de pes costan 5 motons, que costa lo quintal. Resposta: multiplica 100 liuras que fan lo quintal, multiplica per 5 que es son contrari, monta 500,per 7 ne ve 71 $\frac{3}{7}$, manuscrich: 7 $\frac{1}{7}$ aytant valen.

Item 1^a liura de pes costa 5 motons, que costan 5 onsas. Resposta: digas si 16 onsas que fan la liura me donan 5 motons, quant me daran 5 onsas, multiplica 5 onsas per 5 motons, montan 25,per 16 onsas, ne ve 1 & $\frac{9}{16}$, et aytant valen las 5 onsas.

Et aixi se poden fer totas las autras rasons com es dit avisant se del nombre rot si ne avia.

Reglas brevas contengudas en la regla de 3, per saber prestament si la carga costa tant, que costa la liura. Et si la liura costa tant, que costa la carga?

Per autra regla & practica breva & presta deves saber quant la carga costa tant, que costa la liura.

Et quant la liura costa tant, que costa la carga dona las

reglas seguens.

Per las liuras.

1 carga = 3 quintals = 300 liuras de pes;
1 liura d'argent = 20 soutz = 240 deniers;
$\frac{240}{300}$ = $\frac{4}{5}$ Per cascuna liura que costa la carga, la liura del pes ve a $\frac{4}{5}$ de denier.

Per los souses.

Per los souses: per cascun sou que costa la carga, la liura del pes ve a $\frac{4}{5}$ per los deniers.

Per cascun denier que costa la carga la liura ve a $\frac{1}{300}$ de denier.

Nota la practica d'aquestas 3 reglas.

Et per so multiplica las liuras que costa la carga per 4, et apropper 5 et so que ne vendra seran los deniers que val la liura. Itemlos florins per 25 et so que ne vendra seran las 25 mas de deniers.

Item los deniers per 300 et seran 300 mas de deniers.

Nota per ajustar aquells
3 nombres rotz

Et sapias que si tu avias aquells 3 nombres rotz que per ajustar los tu atrobaras $\frac{1}{5}$ en 25 et 25 mas, atrobaras en 300 et per conseguent $\frac{1}{5}$. Et per so multiplica lo nombrador del $\frac{1}{5}$ et lo nombrador de las 25 mas per 12. Et seran totz 300 mas, las quals poyras totas ensemps partir per 300, et sera feyt.

Eyxemple de totas aquestas reglas.

Una carga de pebre costa 37 liuras, que costa la liura? Resposta: multiplica 37 per 4, monta 148,per 5, ne ve 29 & $\frac{3}{5}$, et 29 deniers et $\frac{1}{5}$ de denier costa la liura..

Item 1 carga de pebre costa 37 liuras & 15 souses, que costa la liura? Resposta: multiplica 37 per 4, monta 148,per 5, ne ve 29 $\frac{3}{5}$, que son deniers. Item15 souses per 25, ne ve $\frac{15}{25}$ de denier. Ajusta ho ab aquo de davant, monta 30 deniers & $\frac{1}{5}$ de denier & aitant val la liura.

Item 1 carga de pebre costa 37 liura e 13 souses e 7 deniers, que costa la liura? Resposta: multiplica 37 liuras per 4, monta 148,per 5, ne ve 29 $\frac{3}{5}$. Item13 souses per 25, ne ve $\frac{13}{25}$. Item7 deniers per 300, ne ve $\frac{7}{300}$. Et aixi la liura costa 29 deniers $\frac{3}{5}$ [+] $\frac{13}{25}$ [+] $\frac{7}{300}$ de denier.

Per ajustar aquestz 3 nombres rotz, premierament multiplica 3 per 60, monta 180 que son $\frac{180}{300}$. Item multiplica 13 que son $\frac{13}{25}$ per 12, montan 156, que son $\frac{156}{300}$, de denier. Item ajusta aquells nombres so es 7 et 180 et 156, montan 343,per 300, ne ve 1 & restan $\frac{43}{300}$, ajusta lo denier entier ab los entiers et ve la liura a 30 deniers $\frac{43}{300}$ de denier.

Per saber quant la liura costa tantz deniers, quantas liuras costa la carga? Tu deves saber que a la $\frac{1}{4}$ del denier que costa la liura, ajusta sobre totz los deniers demostra las liuras demanda que costa la carga. Eyxemple. 1^a liura de pebre costa 12 deniers, quant costa la carga? Resposta

la $\frac{1}{4}$ de 12 son 3, ajusta 3 sobre 12, fan 15, et 15 liuras costa la carga quant la liura costa 12 deniers.

Item 1^a liura de pebre costa 19 deniers, que costa la carga? Resposta: la $\frac{1}{4}$ de 19 es 4 et $\frac{4}{3}$, ajusta sobre 19, monta 23 $\frac{3}{4}$ et 23 liuras $\frac{3}{4}$ costa la carga quant la liura costa 19 deniers.

Regla per saber quant la carga costa tantz motons, ho tantz escutz, que costa la liura.

Per saber la regla desus dita mulitplica lo escutz o los motons que costa la carga per las doblas entieras que valen, apropper 30 et so que ne vendra seran los deniers que val 1^a liura, la dobla contant per 10 deniers & non plus & si los escutz o los motons valian plus que per las doblas entieras, multiplica los escutz o los motons que costa la carga al pretz per que auras feyt las doblas per los deniers que valen mais que per doblas entieras et so que ne vendraper 300 et seran 300 mas de deniers.

Et si aprop que tu auras partit per 30 las doblas entieras lo te restava res, multiplica o per 10 & seran 300 mas de deniers, las quals ajusta ab las autras dels deniers e sera feyt.

Un exemple: 1^a carga de pebre costa 7

motons 718 doblas & 5 deniers, que costa la liura? Resposta: premierament multiplica 7 motons per 18 doblas entieras monta 126,per 30, ne ve 4 & restan 6. Item multiplica 7 motons per 5 deniers que val mais que per doblas entieras monta 35,per 300 ne ve $\frac{35}{300}$ et car desus te eran restatz 6 multiplica los per 10 montan 16?, ajusta ab 35 son $\frac{95}{300}$ lo qual nombre si lo abrevias mais que per 5 ve $\frac{19}{60}$. Et costaria doncas la liura 5 deniers et $\frac{19}{60}$ de denier et es feyt.

La regla dels escutz & dels motons.

Et nota que aquest exemple val per so que 10 es $\frac{1}{30}$ de 300 per que se segueis una autra regla que es tala & es general.

Que per cada 10^na que hom an en lo pes quantz los pes son de blatz que en lo partidor ha 1 et per so si eran 2 quintals, lo partidor son 2 et de 1 quintal lo partidor es 10 et de 7 lo partidor es 70 & aixi meteys dels autres nombres.

Nota per atrobar aquestas petitas reglas.

Deves saber que totas aquestas reglas brevas se atroban en la [re]gla de 3, disent si 1 val 1 & aixi aprop abreviant lo nombre rot per sa valor fins a 1 denier.

Siec se la regla que se

apella la regla de diversas formas contengudas en la regla de 3 simpla per la qual se fan las rasons de companhia et diversas autras causas.

Per cascuna multiplica et per totas ensemps parteys.

Et per donar cognoyssensa d'aquesta regla en diversas manieras pot servir & ajudar.

Et premierament en feyt de companhia 3 merchans fan companhia ensemps lo premier met 9 escuts et lo 2: 7 & lo 3: 5, totz 3 an gasanhat 13 escuts, demandi quant ne deu aver cada un del gasanh. Resposta: ajusta las 3 summas que an metudas so es 9, 7, 5, montan 21 que es lo partidor comu. Aras per lo premier multiplica 13 per 9 monta 117 per 21 ne ve 5 et $\frac{12}{21}$ et aquo es lo dreit del premier. Et per lo 2, multiplica 13 per manuscrich: multiplica 3 per 7 montan 21per 9 ne ve 2 et $\frac{3}{21}$ 7 montan 91,per 21 ne ve 4 et $\frac{7}{21}$ et aquo es lo dreyt del 2. Item multiplica 13 per 5, monta 65,per 21 ne ve 3 et $\frac{2}{21}$ et aquo es lo dreyt del 3. Et aissi se fan de totas las autras rasons senblantz.

Nota la prova de las senblans rasons.

Per provar la rason feyta & totas aquellas que se fan per la regla dicta, regarda la companhia de 1^a summa mesa

a las autras mesas. Car tal deu esser la comparansa de las summas que lor pertocan de la devesion.

Como per exemple en la rason feyta tal comparansa es de 9 et de 7 ella es 1 et $\frac{2}{7}$ et tal es de 5 a 7 $\frac{12}{21}$ a 4 et $\frac{7}{21}$. Item tal comparansa es de 9 a 5 ella es 1 et 5 et tal es de 5 et $\frac{12}{21}$ a 3 et $\frac{2}{21}$. Et aysso la plus perfieta prova que se puesca fer en tals rasons.

Nota per la regla desus dita

Per aquestas rasons de companhia es de saber que quant hi a temps hom deu multiplicar la moneda per son temps. Et d'aquella summa de la multiplicatio hom deu far la summa d'aquell que avia metuda la moneda per aquell temps. Exemple: pausi 3 merchans fan companhia ensemps; lo premier met 34 escuts et demora hi 7 meses. Lo 2 met 26 escuts e demora hi 5 meses; lo 3 met 42 escuts et demora hi 3 meses. Et a cap de temps atroban de gasanh 200 escuts. Demandi com se deu partir? Resposta: per lo premier multiplica 34 per 7 meses que hi a demorat, monta 238 que sera la summa que hi a metut lo premier. Item per lo 2 multiplica 26 escuts per 5 meses que hi a demorat, monta 130 que sera

la summa que hi a metut lo 2. Item per lo 3, multiplica 42 escuts per 3 meses que hi a demorat, monta 126 que sera la summa que hi a metuda lo 3 . Aras per saber ta rason ajusta las 3 summas so es 238 et 130 et 126, monta 494 que sera lo partidor comu. Aras per lo premier multiplica 200 per 238 que monta 47600, per 494 que ne ve 96 et $\frac{176}{494}$ et aysso es lo dreyt del premier. Item per lo 2 mutiplica 200 per 130 que monta 26000, per 494 que ne ve 52 et $\frac{312}{494}$ et ayso es lo dreyt del 2. Item per lo 3 multiplica 200 per 126 que monta 25200,per 494, que ne ve 51 et $\frac{6}{494}$ et es feyta la rason per lo tertz.

Tres merchans fan companhia ensemps, lo premier met 200 motos et demora hi 15 meses, lo 2 hi met 94 motons et hi demora 17 meses, lo 3 hi met 38 motons et hi demora 10 meses; et a cap de temps troban en gasanh 400. Demandi com se deven partir? Resposta: per lo premier multiplica 200 motons per 15 meses que hi an istat montan 3000 que sera la summa ha mes lo premier. Item per lo 2 multiplica 94 motons per 17 meses que hi an istat, monta 1598

que fa la summa que metut lo 2. Item per lo 3 multiplica 38 motons per 10 meses que hi a demorat que monta 380 que sera la summa que hi a metut lo 3. Aras per saber ta rason ajusta las 3 summas so es 3000 et 1598 et 380 monta 4978 que sera ton partidor comu. Aras per lo premier multiplica 400 per 3000 que monta 1200000,per 4978 que ne 241 et $\frac{302}{4978}$. Et aquo es lo dreyt del premier. Item multiplica per lo 2 400 per 1598 que monta 639200,per 4978 que ne ve manuscrich: 281 et $\frac{302}{4978}$ 128 et $\frac{2016}{4978}$ et aysso es lo dreyt del 2. Item per lo 3 multiplica 400 per 380 que monta 152000,per 4978 que ne ve 30 et $\frac{2660}{4978}$ et aysso lo dreyt del tertz.

Dus merchans fan companhia ensemps lo premier met 9 escuts et hi demora 4 meses. Lo 2 met 7 escuts et demora hi 6 mes. A cap de temps troban de gasanh 10 escuts. Demandi com se deven partir? Resposta: per lo premier multiplica 9 per 4 meses que hi a demorat monta 36 que sera la summa que hi a metut lo premier. Item per lo 2 multiplica 7 per 6 meses que hi a demorat, monta 42, que sera la summa que hi a metut lo 2. A

per saber la rason ajusta las 2 summas so es 36 et 42, montan 78, que sera lo partidor comu. Aras per lo premier multiplica lo per 36 que monta 360,per 18 ne ve 4 et $\frac{48}{78}$. Et aquo es lo dreyt del premier. Item per lo 2, multiplica 10 per 42, monta 420,per 78, ne ve 5 et manuscrich: 4 et $\frac{108}{78}$ $\frac{30}{78}$. Et aysso es lo dreyt del 2 & aixi meteis de sos senblans.

Item 2 merchans fan companhia ensemps lo premier deu metre 100 escuts et non ne met si non 60. Et lo 2 ne deu metre 80 escuts et ne met si non 60; et atroban que ells an de gasanh 10 escuts. Demandi com se deven partir segont que ell an metut et devian metre. Resposta: per lo 1 tu deves regardar quina part es 60 de 100 que·n devia metre que son $\frac{3}{5}$. Item per lo 2 quina part son 60 de 80 que devia metre que son $\frac{3}{4}$. Et aixi que lo premier ha mes $\frac{3}{5}$ et lo segont $\frac{3}{4}$. Aras per fer ta rason redusis $\frac{3}{5}$ et $\frac{3}{5}$, montan los $\frac{3}{5}$ 12 et los $\frac{3}{5}$ montan 15, ajusta tot monta 27 que sera lo partidor comu. Aras per lo premier multiplica 10 per 12 monta 120, per 27 ne ve 4 et $\frac{12}{27}$. Item per lo 2 multiplica 10 per 15 que monta 150,per

27 ne ve 5 et $\frac{15}{27}$ et aixi de senblans.

Item son 2 merchans que fan conpanhia per 3 ayns. Lo premier deu metre 100 et non ne met mas 60 et dels 3 ayns que deu istar non n'i ista si non 2. Lo 2 n'i deu metre 80 et non n'i met mas 60 et de 3 ayns que lo devia istar non n'i a istat [non] 1 $\frac{1}{2}$. Et an gasanhat 30. Demandi com se deu partir segont que an metut & et devian metre & lo temps que han istar et ho devian istar. Resposta: per lo premier quinas partidas son so que an metut & devian metre et lo temps que hi devian istar et an istat com es istat feyt. En la rason desus de la moneda que avian metuda & devian metre l'argent del premier $\frac{3}{5}$ & son temps es $\frac{2}{3}$. L'argent del 2 es $\frac{3}{4}$ et son temps es $\frac{1}{2}$. Aras multiplica l'argent per son temps. Et digas per lo premier $\frac{2}{3}$ contra $\frac{3}{5}$ son $\frac{6}{15}$ que valen $\frac{2}{5}$. Aprop digas per lo 2 $\frac{1}{2}$ contra $\frac{3}{4}$ que

son $\frac{3}{8}$. Et aixi lo premier ha metutz $\frac{2}{5}$. Et lo segont $\frac{3}{8}$ et an gasanhat 30. Redusis $\frac{2}{5}$ et $\frac{3}{8}$, montan los $\frac{3}{5}$ que a metutz lo segont montan 15. Aras per lo premier multiplica 30 per 16 montan 480,per 31 que son las 2 summas et lo partidor comu que * Item per lo 2 multiplica
30 per 15 monta
450,per 31
que ne ve 14 et $\frac{16}{31}$ ne ve 15 & $\frac{15}{31}$.* Et es feyta la rason et en tal maniera se fan las senblans rasons.

Item 2 merchans fan companhia ensemps. Lo premier avia metut 140 liuras et l'autre 20 pessas de drap. Et atroban que an gasanhat 180 liuras del qual gasanh pertocan en aquell dels 20 draps 180 liuras. Demandi quant valian las 20 pessas dels draps. Resposta & per la regla de 3, tu deves levar 180 de 300, restan 120 que son d'aquell que avia metut 140 liras, digas aras si 120 me venen de 140 que avias de quant me vendran 180 per multiplica 180 per 150, montan 27000,per 120 que ne ve 225; doncas 225 valian las 20 pessas del drap.

Item son 3 merchans que fan companhia ensemps. Lo premier met 180 florins, lo 2 met 500 liuras de moneda, lo 3 met 2500 liuras de lana. Et a cap de temps atroban en gasanh 460 florins. Lo premier manuscrich: casanh deu aver del gasanh 120 florins. Lo 2 ne deu aver per sa partida 130 florins. Et lo 3 ne deu aver 210 florins. Demandi quantas liuras de moneda valen los que avia metutz lo premier. Et quantas liuras de moneda valen las 2500 liuras de lana que ha mes lo tertz. Resposta: per la regla de 3, lo gasanh de las liuras de la moneda te mostrara la valor dels florins et de las liuras de la lana en las liuras de la moneda. Et per so digas: per lo premier si 130 florins me venen de 500 de moneda, de quant me vendran 120 florins que pertocavan al premier; multiplica 120 per 500 que montan 60000,per 130 que ne ve 461 et $\frac{70}{461}$. Et tantas liuras de moneda valen 180 florins. Item digas per lo 3 si 130 florins me son vengutz de 500 liuras de moneda de quant me vendran 210 florins que pertoca al tertz; multiplica 210 florins per 500 liuras de moneda que monta 105000,per 130 que ne ve 807 & $\frac{90}{130}$, et aytantas liuras de moneda valen las 2500 de la lana que aura mes

per lo tertz, et es feyt.

Item son 3 merchans que an feyt 1 companhia ensemps. Lo premier ha metutz 280 florins et lo 2 a metutz 300 florins; del tertz no se sap que a metut; atroban en gasanh 800 del qual gasanh s'en pertoca al tertz del qual non sap hom que ha metut 250 et als autres tot lo romanent. Demandi que ha metut lo tertz? Resposta: leva del gasanh comu lo gasanh del tertz, restan 550 que fera ton partidor. Item ajusta las 2 summas dels 2, so es assaber 280 et 300 que montan 580. Aras digas per la regla de 3: si 550 de gasanh que me son vengutz de 580 que avian metut los 2, de quant me vendran 250 que pertocan al tertz? Multiplica * manuscrich: 252 250* per 580 que montan 145000,per 550 que ne ve 263 et 550. Donc avia metut lo tertz 263 florins et $\frac{350}{550}$ de flori.

Item 1 merchant fa tal convenent ab son factor: yeu te baylle 400 liuras de moneda de present que las governes per 5 ayns et a cap de 5 ayns las 400 liuras sien tieuas de tot et lo gasanh que auran feyt sera myeu. Se endeven que lo factor a governat las 400 liuras 3 ayns et $\frac{1}{2}$ et non plus et atroban de gasanh 600 liuras; demandi com deu esser pagat lo factor et

que deu aver lo maistre que deguns dels non sie deceuput. Resposta: per la regla de 3. Si lo factor agues complit son temps ell agra gasanhat las 400 liuras; per so digas si 5 ayns me donan 400 liuras quant me daran 3 ayns et $\frac{1}{2}$? Multiplica 3 ayns et $\frac{1}{2}$ per 400 que montan $\frac{2800}{2}$, per 5 ayns et premierament redusis et digas 2 vegadas 5 son 10, aras 2800 per 10 que ne ve 280 et aytant deu aver lo factor et lo sobreplus de 800 que son 520 es del merchant & mais las 400 liuras que que avia bayllat al factor.

Item 1 merchant ha bayllat 600 liuras a 1 factor lo qual deu aver 200 liuras ab tal convent que trabalhe ab aquestas 800 liuras per 5 ayns; et al cap del temps nos partirem per lo mieg lo principal et lo gasanh. Esdeve se que lo factor non met pont de las 200 liuras res, mas aver menat las 600 liuras del merchant; et a cap de 5 ayns atroban 2400 liuras contant lo principal ab lo gasanh. Demandi com se deu fer aquell partiment, attendut que lo factor no hi a mes so que hi devia

metre, que lo merchant non sie deceuput. Resposta per la regla de 3: premierament digas si 600 liuras que avia metut lo merchant an gasanhat 1800 liuras que agran gasanhat 200 liuras que devia metre lo factor? Multiplica 200 per 1800 que montan 360000, per 600 que ne ve 600 et aytant agran gasanhat, ajusta son principal que es 200 et son gasanh que es 600 ab lo principal et ab lo gasanh del merchant que es tot 2400 que monta 3200, arasper lo mieg que ne ve 1600 et aytant ne aura lo merchant et lo romanent es per lo factor que es 800 et es feyta la rason.

Item 1 merchant ha una pessa de mescla en la qual ha 6 onsas d'aur & d'argent 5, de coyre n'i a 4; et ne leva 9 onsas per far 1^a tassa. Demandi quant aura en la tassa d'aur n'i quant d'argent, n'i quant de coyre? Resposta ajusta los 3 metals que montan 15 que es lo partidor comu. Aras per saber quant hi a d'aur, multiplica 9 per 6 que monta 54, per 14 que ne ve 3 $\frac{9}{15}$ d'onsas. Doncx 3 et $\frac{9}{15}$ de onsa hi aura de aur. Item per saber

d'argent, multiplica 9 per 5 que son 45,per 15 que ne ve 3 et 3 onsas hi aura d'argent. Item per saber quant hi aura de coyre, multiplica 9 per 4 que montan 36,per 15 que ne ve 2 et $\frac{6}{15}$ et 2 onsas & $\frac{6}{15}$ de onsas hi aura de coyre.

Sieguen se los exemples de las 3 partidas de la regla de 3 que son ab temps, mesura & pes. Et de la cascuna donarey 3 exemples. La 1 en temps et l'autre en mesura. Et l'autre en pes. Et de la tersa davantage un de 3 monedas diversas et un de 3 causas diversas.

manuscrich: 11 Premierament yeu demandi si 6 escuts en 4 meses gasanha 3 souses, 7 escuts en 5 meses quant gasanharan? Resposta: premierament tu deves multiplicar l'argent per son temps et per so digas: 6 escuts contra 4 meses montan 24. Item mais 7 escuts contra 5 meses montan 35. Aras digas per la regla de 3, si 24 me donan 3 sous quant me daran 35 escuts? Multiplica 35 escuts que voles saber per 3 souses que es son contra, montan 105,per 24 escuts que son senblant que ne ve 4 et $\frac{9}{24}$ de souses gasanharan los 7 escuts en 5 meses et aixi fases totz fes senblans.

Exemple de mesuras. Cant 1^a pessa de drap costa 9 motons. Et 2 can[n]as costan 12 gros d'aquell drap, demandi si aquell se encaresteys[?] per ve que la pessa coste 12 motons que costaran las 3 cannas? Resposta: multiplica l'argen[t] per sa mesura. Et digas per lo premier 2 vegadas 9 son 18. Item per lo segont 3 vegadas 12 son 36. Aras digas si 18 me dona 12, quant me daran 36? Multiplica 36 per 12 que monta 432,per 16 manuscrich: 24 que ne ve 27, donc 27 gros montarian las 3 cannas quant la pessa costaria 12 motons. Et aixi de sos senblans.

Exemple de pes: quant lo sestier del blat costa 9 gros hom fan 1 pa que pesa 12 onsas, lo qual costa 2 deniers. S'esdeve que lo blat puja a 12 gros. Demandi quant val lo pa que pesava 15 onsas. Resposta: premierament multiplica l'argent per lo pes. Et digas per lo premier 9 vegadas 12 son 108. Item per lo segont 12 vegadas 15 monta 180. Aras digas: si 180 me donan 12 que me daran 180? Multiplica 180 per 2 que me daran 360,per 108 que ne ve 3 et $\frac{36}{108}$

que valen $\frac{1}{3}$. Doncx 3 & $\frac{1}{3}$ costa lo pan que pesa 15 onsas quant lo blat sera vendut 12 gros.

Exemple de temps

Item si 6 escuts en 4 meses gasanhan 3 sous demandi 7 escuts en quant de temps los gasanharan. Resposta: multiplica 6 per 4 meses que montan 24, per 7 que ne ve 3 & $\frac{3}{7}$ et en 3 meses & $\frac{3}{7}$ de mes los gasanharan.

Item quant 1^a pessa de drap costa 9 motos, las 2 cannas d'aquell drap costan 12 gros. Demandi quant deuriam aver d'aquell drap per aquells 12 gros quant la pessa meteyssa costara 12 motos. Resposta: multiplica 9 motos per 2 cannas, monta 18,per 12 ne ve manuscrich: $\frac{12}{6}$ 1 et $\frac{6}{12}$ que vale $\frac{1}{2}$ et 1^a canna & $\frac{1}{2}$ aura per 12 gros quant la pessa seria veduda a 12 motos.

Exemple de pes.

Item quant lo blat costa 9 gros lo sestier lo pa que pesa 12 onsas costa 2 deniers. Demandi quant deuria pesar si lo blat costa 12 gros. Resposta: multiplica 9 per 12, que monta 108,per 12 que ne ve 9, et 9 onsas deuria pesar lo pan de 2 deniers quant lo blat serie vendut a 12 gros.

Los exemples de la 3 partida

Si 6 escutz en 4 meses gasanha[n]

3 souses, 7 escutz en quant de temps gasanharan 5 souses? Resposta: multiplica 5 souses que voles saber per la multiplicatio de 6 escutz ab 4 meses que monta 24, et digas 24 vegades 5 son 120, que deves partir per la multiplicatio de 3 souses contra 7 escutz que montan 21; doncas 120 per 21, que ne ve 5 & $\frac{15}{21}$, que valen $\frac{5}{7}$ et en 5 meses & $\frac{5}{7}$ de mes gasanhan lo[s] 7 escuts, 5 souses et es feyt.

Exemple de mesura. Quant 1 pessa de drap costa 9 motos, las 2 cannas d'aquell drap costan 12 gros. Demandi quant aquella pessa de drap vendria a 12 motos, quant ne auria hom per 15 gros? Resposta: multiplica 15 gros que voles saber per 18 que es la multiplicatio de 9 motos contra 2 cannas, que montan 270, que deves partir per la multiplicatio de 12 gros contra 12 motons, que montan 144,doncas 270 per 144 que ne ve 1 et $\frac{126}{144}$, que valen $\frac{7}{8}$, donc 1 canna et $\frac{7}{8}$ de canna d'aquell drap aurie hom per 15 gros quant la pessa de 9 motos serie venduda a 12 motos. Et en aquell pretz que quant la pessa costa 9 motons las 2 cannas costaran 12 gros.

Exemple de pes.

Quant lo sestier del blat costa 9 gros hom fa lo pa que pesa 12 onsas que costa 2 deniers. Demandi: quant lo blat costaria manuscrich: pesar 12 gros, quant deura costar lo pa que

manuscrich: deniers pesara 15 onsas. Resposta: premierament multiplica l’argent per lo pes & digas per lo premier 9 vegadas 12 son 108. Item manuscrich: 180 per lo segont 12 vegadas 15 son 180. Si 108 me donan 2, que me daran 180? Multiplica 180 per 2, que son 360,per 108, ne ve 3 & $\frac{36}{108}$, que valen $\frac{1}{3}$, doncs 3 deniers et $\frac{1}{3}$ costa lo pa que pesa 15 onsas quant lo blat sera vendut 12 gros.

Los exemples de la 3 partida.

Si 6 escutz en 4 meses gasanhan 3 souses, demandi 7 escutz, en quant de temps los gasanharan? Resposta: multiplica 6 per 4 meses, que montan 24,per 7 escutz [*] [*] que ne ve 3 et $\frac{3}{7}$ et en 3 meses & $\frac{3}{7}$ de mes los gasanharan.

Exemple de mesuras

Quant 1^a pessa de drap costa 9 motos, las 2 cannas d'aquell drap costan 12 gros. Item demandi quant deurem aver d'aquell drap per aquells 12 gros quant la pessa meteyssa costara 12 motons. Resposta: multiplica 9 motons per 2 cannas, montan 18,per 12, que ne ve 1 et $\frac{6}{12}$ manuscrich: $\frac{12}{6}$ , que vale $\frac{1}{2}$ et 1 canna et $\frac{1}{2}$ aurien per 12 gros quant la pessa serie venduda a 12 motons.

Exemple per pes.

Quant lo blat costa 9 gros lo sestier, lo pa que pesa 12 onsas costa 2 deniers; demandi quant deuria pesar si lo blat costa 12 gros. Resposta: multiplica 9 per 12 onsas, que montan 108,per 12, que ne ve 9, et 9

onsas deu pesar lo pa de 2 deniers quant lo blat serie vendut a 12 gros.

Los exemples de la 3 partida.

Si 6 escuts en 4 meses gasanhan 3 souses, 7 escuts en quant de temps gasanharan 5 souses? Resposta: multiplica 5 souses que voles saber per la multiplicatio de 6 escuts ab 4 meses que montan 24 et digas: 24 vegadas 5 son 120, que deves partir per la multiplicatio de 3 souses contra 7 escuts que montan 21,doncas 120 per 21 que ne ve5 et $\frac{15}{21}$ que valen $\frac{5}{7}$ et en 5 meses & $\frac{5}{7}$ de mes gasanharan los 7 escuts 5 souses.

Exemple de mesura.

Quant 1^a pessa de drap costa 9 motos, las 3 cannas d'aquell drap costan 12 gros. Demandi quant aquella pessa de drap vendria a 12 motos, quant ne aurien per 15 gros? Resposta: multiplica 15 gros que voles saber per 18 que es la multiplicatio de 9 motos contra 2 cannas que montan 270 que deves partir per la multiplicatio de 12 gros contra 12 motos que montan 144; partes doncas 270 per 144 que ne ve 1 et $\frac{126}{144}$ que valen $\frac{7}{8}$. Donc 1^a canna & $\frac{7}{8}$ de canna d'aquell drap aurien per 15 gros quant la pessa de 9 motos serie venduda a 12 motos et en aquell pretz que quant la canna costa 9 motos las 2 cannas costan 12 gros.

Exemple de pes.

[*] lo sestier Quant lo blat costa 9 gros [*] hom fan pa que pesa 12 onsas que costa 2 deniers. Demandi quant lo blat costaria 12 gros quant deuria pesar lo pa que coste 5 deniers. Resposta: multiplica

5 deniers que voles saber per 378 que es la multiplicatio de 9 gros contra 12 onsas que montan 540, que deves partir per 24 que es la multiplicatio de 2 deniers contra 12 gros;doncas 540 per 28 que ne ve 22 et $\frac{12}{24}$ que valen $\frac{1}{2}$ et 22 onsas & $\frac{1}{2}$ deuria pesar lo pa de 5 deniers quant lo blat costarian 12 gros a la rason que quant costava 9 gros lo pa de 2 deniers pesava 12 onsas.

Exemple de 3 monedas.

Quant 3 deniers de Perpenha valen 5 deniers de Montpellier et 2 de Montpellier valen 3 d'aquells d'Avinho, demandi 12 d'aquells d'Avinho quantas ne valen d'aquells de Perpenha? Resposta: multiplica 12 que voles saber per 6 que es la multiplicatio de 3 deniers de Perpenha et 2 de Montpellier que sabes que valen, que monta 72,per 15 que es la multiplicatio de las monedas que restavan desus que ne ve 4 & $\frac{12}{15}$ que valen $\frac{4}{5}$ et 4 deniers et $\frac{4}{5}$ de deniers de Perpenha valen los 12 d'Avinho.

Exemple de 3 causas diversas.

Quant 3 cannas de drap valen 7 motos et 9 motos valen 5 liuras de la moneda de Perpenha, demandi 6 cannas d"aquell drap quantas liuras de Perpenha valen? Resposta: multiplica 6 cannas que voles saber per 35 que es la multiplicatio de 7 motos ab 5 liuras que monta 210,per 27 que

es la multiplicatio de las 2 causas que restan desus so es 3 et 9 que ne ve 7 et $\frac{21}{27}$ que valen $\frac{7}{9}$; donc las 6 cannas del drap valen 7 liuras & $\frac{7}{9}$ de liura de la moneda de Perpenha.

Nota per saber lo contrari atrobar.

Per la tersa partida de la regla deves saber que en las causas que montan & devallan com es temps, pes & mesura que la multiplicacio que ne ve d'aquells ab lurs monedas es multiplicador contra lo gasanh o la valor que voles saber & en las autras causas diversas com son los 2 exemples detras la multiplicacio que ve del plus contrari que es tot solet ab lo equivalent del senblant de so que voles saber es multiplicador contra so que voles saber.

Et nota que totztemps la questio es del plus contrari que es tot solet et per conseguent la resposta es d'aquell.

Nota per saber  tornar tot a la premiera partida.

Per las 3 partidas de la regla es de saber que las 2 retornan en la premiera, car la 2 se retorna en la 3 et se retorna en la premiera, la 3 se retorna en la 3 escrivent 2 vegadas 1 gasanh ho una valor. Com si eran diversas disent 6 escutz en 4 meses gasanhan 3 souses 7 escutz en quant de temps gasanhan 3 souses et aissi dels autres

La tersa se retorna a la premiera.

fasent 1^a summa de la multiplicacio que deu esser lo multiplicador & aquella es lo contrari en una autra summa de la multiplicatio que deu esser partidor et aquella es so que hom sap. Como per exemple 6 escutz en 4 meses gasanhan 3 souses, 7 escutz en quant de temps gasanharan 5 souses? 5 souses es so que voles saber & 24 es son contrari, 21 so que saber voles perque deves metre en la premiera partida de la regla disent si 21 me dona 24 que me daran 5 souses? Et aixi aprop que aquellas 3 reglas non son mas una regla que es de la premiera.

Notas practicas de la regla de 3.

Deves saber que aquesta regla de 3 se pot fer en 3 manieras, la 1 es aquella que es dicta que es multiplicar so que hom vol saber per son contrari & partir per son senblant. La 2 es que hom deu partir lo contrari per so que hom sap et so que ne vendra multiplicar per so que hom vol saber. Exemple: 4 escutz valen 9 motos, que valen 7 escutz? Resposta: 9 motons per 4 escutz, que ne ve 2 & $\frac{1}{4}$, que deves multiplicar per 7 escutz que voles saber. Et aquesta seconda maniera a rason per so que hom sap premierament quant val 1, la qual causa se sap quant hom loper lo contrari per so que hom sap et segont que val 1, hom

sap aquo que hom vol saber e aysso per la multiplicatio. La 3 es que hom deu gardar so que hom vol saber de so que hom sap. Et aisso pendre en lo contrari. Exemple: 6 escutz valen 10 motos, que valen 4 escutz? Resposta: que es 4 de 6? que son $\frac{2}{3}$, perque pren $\frac{2}{3}$ de 10, car aytant valen. Item 12 valen 17, que valen 15? Resposta: en 35 ha 12 vegadas que son 2 vegadas 17. Item restan 6, 4, 1 que son $\frac{1}{2}$ & $\frac{1}{3}$ de $\frac{1}{12}$ que 12, valen la $\frac{1}{2}$ et $\frac{1}{3}$ et la $\frac{1}{2}$ de 17. Et aquesta regla ha rason como lo tot val lo tot, la $\frac{1}{2}$ val la $\frac{1}{2}$ & lo $\frac{1}{3}$ val lo $\frac{1}{3}$ et lo $\frac{1}{4}$ val lo $\frac{1}{4}$ & aixi de las autras partidas. Et per saber que es que voles saber de so que sabes, parteys so que voles saber per so que sabes car so que ne vendra lo demostrara. E si voles saber so que deves pendre que monta en lo contrari multiplica lo contrari per so que te es vengut del partir quant as partit so que volias saber per so que sabes car la multiplicatio te ho mostrara.

La premiera partida..

manuscrich: escutz=6

meses temps

escuts	meses	souses	escuts	mes
11	4	3	7	5

mesura

motos	cannas	grosses	cannas
9	2	12	3

pes

grosses	onsas	deniers	grosses	onsas
9	12	2	12	15

La 2 partida.

temps

escutz	meses	souses	escutz
6	4	3	7

manuscrich:
cannas=12
grosses=2

mesura

motos	cannas	grosses	motos
9	2	12	12

pes

grosses	onsas	deniers	grosses
9	12	2	12

La 3 partida.

manuscrich: souses=5 oblidada

temps

escutz	meses	souses	escutz	souses
6	4	3	7	5

manuscrich: cannas=2

mesura

motos	cannas	grosses	motos	grosses
9	3	12	12	15

pes

grosses	onsas	deniers	grosses	deniers
9	12	2	12	5

monedas

Perpenha	Montpellier	Montpellier	Avinho	Avinho
3	5	2	3	12

causas diversas

cannas	motos	motos	liuras	cannas
3	7	9	5	6

Et aissi atermena la regla de 3..

Siec se la 2 regla general que se appella del falsa positio ab diverses exemples.

Pueys que hey tractat de la regla de 3 que es la premiera regla general et plus comuna a merchans, resta que yeu tracte de la 2^a regla de 1^a falsa positio, la quall aura 2 partidas, la premiera se fay ajustant, partent & sustraent. Et aquella non fay pas raso necessaria car per cada nombre que muda et fa raso, muda [la] resposta.

La 2 se fa per multiplicatio & devisio & fa sa rason necessaria car fa totztemps 1^a resposta de la qual lo darey de diverses exemples. Et

premierament donant la regla que es tala.

Pausa 1 nombre qual que tu vulhas sobre lo qual tu atrobaras nombres dels quals levadas que ne fossan las partidas prepausadas aquell nombre resta entierament. Los quals sobre ell trobas totz ensemps sens ell ajustatz se partiscan per 1 mens que non son aquels en los quals se deu fer la raso et de so que vendra del partiment sustray los nombres atrobatz car so que restara sera lo nombre d'aquell que demanda tal partida quant tu sustrayras lo nombre de ta position, so que restara sera lo pretz que tu voles saber.

Problema ancian conegut en cò dels matemetics chines, arabis, bizantins o europencs. Ex.: Leonard de Pisa. Problema parier en lo Pellos, fol. 64r (Michel Guillemeot) Exemple. 3 homes volen comprar un roci, lo qual costa tant. Et cada un d'els porta tant pauc d'argent que degun d'els per si solet no lo pot comprar. Mas lo 1 ditz als autres 2: Prestatz-me la $\frac{1}{2}$ de tot vostre argent, et ab lo mieu yeu comprarey lo roci. Et lo 2 ditz als autres 2: Prestas-me lo $\frac{1}{3}$ de vostre argent, et yeu ab lo mieu comprarey lo roci. Lo 3 dis als autres: mas me prestatz vosautres lo $\frac{1}{4}$ de vostre argent, et yeu ab lo mieu lo comprarey. Demandi que costa lo roci et que ha cascun d'els d'argent.

Resposta. Yeu pausi per

mon plaser 12. Sobre lo qual nombre per aquell que demanda la $\frac{1}{2}$ atrobi 24; car qui ne levaria la $\frac{1}{2}$ restarian 12. Per lo 2 que demanda lo $\frac{1}{3}$, preni 18; car qui ne leva lo $\frac{1}{3}$ restan 12 & per lo 3 manuscrich: $\frac{1}{3}$! tertz atrobi 16; car qui leva lo $\frac{1}{4}$ restan 12. Ajusta aquellas 3 summas, so es 24, 18, & 16, montan 58; la qual summa devi partir per 2, que es mens 1 que non son los 3 homes, que ne ve 29. Aras per saber quant costa lo roci, leva 12 de 29, restan 17, et 17 costa lo roci.

Item per saber que porta aquell que demanda la $\frac{1}{2}$, leva 24 de 29, restan 5, que porta aquell de la $\frac{1}{2}$. Item per lo 2 leva 18 de 29, restan 11, que porta aquell que demanda lo $\frac{1}{3}$. Item per aquell que demanda la $\frac{1}{4}$ part leva 16 de 29, restan 13, que porta aquell.

Item 4 homes compran un rocin coma manuscrich: lo $\frac{1}{4}$ demanda lo 5 dessus, mas que lo 4 demanda lo $\frac{1}{5}$ del argent dels autres. Demandi com dessus que costa & que porta cada un d'els. Resposta: per mon plaser pausi 60 escutz; per lo premier atrobi 120, per lo 2: 90, per lo 3: 80, et per lo 4: 75. Ajusta totas aquellas summas, so es 120, 90, 80, et 75, que montan 365; partis per 3, que es mens 1 de 4 homes, que ne ve 121 et $\frac{2}{3}$. Aras per saber que val lo roci, leva 60 de 121 et $\frac{2}{3}$, resta 61 et $\frac{2}{3}$, et aitant val. Item per lo premier leva 120 de

121 et $\frac{2}{3}$, resta 1 & $\frac{2}{3}$, et atant portava.

Item per lo 2, leva 19 de 121 & $\frac{2}{3}$, restan 31 et $\frac{2}{3}$, et aitant portava. Item per lo 3, leva 80 de 121 et $\frac{2}{3}$, resta 41 & $\frac{2}{3}$; & tant porta.

Item per lo 4, leva 75 de 121 & $\frac{2}{3}$, restan 46 et $\frac{2}{3}$. Et atant porta.

Exemple de drap.

Item son 5 homes que volen comprar una pessa de drap en tal maniera que lo 1 demanda a totz los autres la $\frac{1}{2}$ de tot l'aur et l'argent que portan los autres; lo 2 demanda lo $\frac{1}{3}$, [lo 3 demanda lo $\frac{1}{4}$,] lo 4 demanda lo $\frac{1}{5}$, lo 5 la $\frac{1}{6}$ part. Demandi que costa la pessa & que porta cascun d'els. Resposta. Per mon plaser pausi 60. Aras per lo 1, yeu atrobi 120, per lo 2, 90, per lo 3, 80, per lo 4, 75. Et per lo 5, 72. Ajusta totz aquestz nombres, ses la positio que es 60, que montan 437, que deves partir per 1 mentz [*] homes los 5 [*] que fan la compra. Partis doncas 437 per 4 que ne ve 109 & $\frac{1}{4}$ del qual nombre leva 60 per saber que costa la pessa, restan 49 et $\frac{1}{4}$; et aytant costa. Aras per lo 1 Primiera mencion coneguda d'una solucion negativa, plenament acceptada leva ne 120, restan 10 & $\frac{3}{4}$ mens de non res. Item per lo 2 leva [ne] 90, resta 19 & $\frac{1}{4}$.

manuscrich: leva ne 57, restan 34 & $\frac{1}{4}$ Item per lo 3 leva ne 80, restan 29 et $\frac{1}{4}$.

Item per lo 4 leva-ne 75, restan 34 et $\frac{1}{4}$. Item per lo quint leva-ne 72, restan 37 et $\frac{1}{4}$.

Et aytant portava cascun d'els como restava en la sustractio de sa summa.

Aras per veser la raso; per lo 1, pren la $\frac{1}{2}$ de la

summa dels autres, monta 60; del qual deves partir per 10 & $\frac{3}{4}$ que lo premier ha mens de non res, restan 49 et $\frac{1}{4}$, que es lo pretz de la pessa. Item per lo segont pren lo $\frac{1}{3}$ de totas las autras summas, que montan ab la sua 52 et $\frac{10}{12}$; leva ne lo $\frac{1}{3}$ de 10 & $\frac{3}{4}$ que lo 1 ha mens de non res, restan 49 & $\frac{3}{4}$, que es lo pretz de la pessa. Item per lo 3 pren lo $\frac{1}{4}$ de totas las autras summas, montan ab la sua 51 et $\frac{15}{16}$; leva ne lo $\frac{1}{4}$ de 10 & $\frac{3}{4}$ que ha lo 1 mens de non res, restan 49 & $\frac{3}{4}$, que es lo pretz de la pessa. Item per lo 4 pren lo $\frac{1}{5}$ de las autras summas, montan a la sua 51 & $\frac{8}{20}$; leva ne 51 de 10 & $\frac{3}{4}$ que ha mens de non res, lo premier resta la valor de la pessa. Item per lo derrier pren lo $\frac{1}{6}$ part de las autras summas, montan ab la sua 51 et $\frac{1}{24}$; leva ne la $\frac{1}{6}$ part de 19 et $\frac{3}{4}$ que ha lo premier mens de non res, restan 99 et $\frac{1}{4}$, que es la valor de la pessa del drap.

Et aquestas rasons suffiscan per aquesta premiera partida de la regla de 1^a position.

Siec se la 2^a partida de la regla de 1^a falsa posicio.

Pausa 1 nombre qual que sie aquell a ton plaser lo qual sie multiplicat per aquesta regla & deves notar que quant sera feyta alcuna questio en que metra $\frac{1}{2}$, $\frac{1}{3}$ & $\frac{1}{4}$ & aissi de las autras que hom deu pausar

1 nombre en lo qual se atroba entierament en las partidas prepausadas. Aysso es per gardar se de pena per causa del nombre rot & non pas que non se feses veper autra maniera mas ab major pena de la qual regla dona alcuns exemples generals que se poden a son perpaus applicar.

Troba 1 nombre que quant tu li auras ajustat sa $\frac{1}{2}$, $\frac{1}{3}$ & son $\frac{1}{4}$, tot non fassa que 9. Resposta: pausa [?] & ajusta 12, 6, 4 et 3, que son las partidas desus dictas ab 12, que montan 25. Aras digas si 25 me son vengutz de 12, de quant me vendra 9? Multiplica 9 que voles saber per 12 que es lo nombre mes, que monta 108, per 25 que te era vengut de la positio que ne [ve] 4 et $\frac{8}{25}$ et aysso es lo nombre.

Item atroba 1 nombre que auras ajustat sobre ell fa $\frac{1}{2}$ & lo $\frac{11}{3}$ de tot & aprop lo $\frac{1}{4}$ de tot. Tot ensemps sinon fa que [?]. Resposta: pausa 6 ajusta la mittat que son 9. Item ajusta lo $\frac{1}{3}$ et son 12. Item ajusta lo $\frac{1}{4}$, son 15. Aras digas: si 15 me son vengutz de 6, de quant me vendran 9? Multiplica 9 que voles saber per 6 que es lo nombre pausat, que monta 54,per 15 que te era vengut de la positio, que ne ve 3 et $\frac{9}{15}$ & aysso es lo nombre que tu demandas. Item atroba 1 nombre del qual ha la $\frac{1}{2}$, $\frac{1}{3}$

non sien que 5. Resposta: pausa 12 del qual la $\frac{1}{2}$ & lo $\frac{1}{3}$ son 10 & digas: si 10 son vengutz de 12, de quant me vendran 5? Multiplica 5 que vole saber per 12 que as mes que monta 60,per 10 que te era vengut de la posicio, que ne ve 6 et aysso es lo nombre que tu voles .

Exemple de sustrayre.

Item nota 1 nombre que quant ne auran levat lo $\frac{1}{3}$ &$\frac{1}{4}$ so que restara sie 3. Resposta: pausa 12 leva ne $\frac{1}{3}$ & lo $\frac{1}{4}$, restan 5 et digas: si 5 me donan 12, de quant me vendran 3? Multiplica 3 que voles saber, per 12 que as metut que montan 36,per 5 que te eran vengutz de la posicio que ne [ve] 7 & $\frac{1}{5}$ & aisso es lo nombre que demandas.

Exemple per multiplicar.

Item atroba 1 nombre que quant tu lo auras multiplicat per 2 & so que ne vendra per 3, et so que ne vendra per 4, et que la derriera multiplicatio non fassa si non 7. Resposta: pausa 3 per ton plaser, multiplica lo per 2, fan 6. Item multiplica 6 per 3, fan 18. Item multiplica 18 per 4, fan 72. Et digas: si 72 me son vengutz de 3, de quant me vendran 7? Multiplica 7 que voles saber per 3 que as metutz que fan 21,per manuscrich: $\frac{21}{27}$ 72, ne ve $\frac{21}{72}$, et aysso es lo nombre.

Per partir, exemple, atroba 1 nombre que qui lo partira per 7 que ne vengan 3 et $\frac{1}{2}$. Resposta: pausa 14, que ne ve 2.

Aras digas: si 2 venen de 14, de quant me vendran 3 & $\frac{1}{2}$. Multiplica 3 $\frac{1}{2}$ que voles saber per 14, monta $\frac{98}{2}$,per 2 que ne ve 24 $\frac{1}{2}$ & 24 $\frac{1}{2}$ es lo nombre que voles saber.

Siec se la applicacio de les exemples generals metutz.

Exemple de ajustar.

Un home ditz si yeu avia aytant mais de temps com ay & la $\frac{1}{2}$ $\frac{1}{3}$ et lo $\frac{1}{4}$ de mon temps sobre ajustat yeu non aurie mas 50 ans; demandi quant ha de temps l'ome. Resposta: pausa 12 per ta positio. Item mais 12 car ha dit aytant mais. Aprop la $\frac{1}{2}$ $\frac{1}{3}$ et lo $\frac{1}{4}$ de 12 que monta 13, ajusta ho tot monta 37. Aras digas: si 37 so vengutz de 12, de quant vendran 50? Multiplica 50 que voles saber per 12 que as metutz, monta 600,per 37 que te eran vengutz de la positio que ne ve [16] $\frac{8}{37}$ et 16 ans et $\frac{8}{37}$ ha l'ome desus dit.

Exemple de sustrayre.

Una lansa ha la $\frac{1}{2}$ $\frac{1}{3}$ en ayga et 9 pams de fora. Demandi quant ha Se retroba en lo Pellos de lonc. Resposta: pausa 12 et $\frac{1}{2}$ de $\frac{1}{3}$ et lo 12 son 10 et restan 2. Digas: si 2 son vengutz de 12 de quant vendran 9? Multiplica 9 que voles saber per 12 que as mes, monta 108,per 2 que te eran vengutz de la posicio , que ne ve 54 & atant a de lonc.

Una pessa de drap ha lomanuscrich: la $\frac{1}{3}$ blanc & lo $\frac{1}{4}$

negre et 8 pams de gris, demandi quant ha de lonc. Resposta: pausa 12 & $\frac{1}{3}$ $\frac{1}{4}$ de 12, son 7 & resta 5. Aras digas si 5 me venan de 12, de quant me vendran 8? Multiplica 8 que voles saber per 12, que as mes, monta 96, partis per 5, que te es vengut de la positio, que ne ve 19 & $\frac{1}{5}$ et 19 pams et $\frac{1}{5}$ de palm ha de lonc.

Un vayssell ha 3 dosils, la 1 major que l’autre & es [tal] que [quant] ubria lo major, tot lo vi ne salhirie en 3 horas. Et qui ubria lo mejancier ne salhirie en 4 horas. Et qui ubria lo mendre, se·n salhirie en 6 horas. Demandi que qui ubrie totz los dosils ensemps, en quant de temps ne salhiria lo vi. Resposta: pausa 12 en que atrobaras 6 ,4 & 3. Entieramentz que son 12 sestiers de vi que te lo vayssell; qui obre lo major, lo ne salhen 4 sestiers per hora. Et qui huebre lo mejancier, lo ne salhen 3 sestiers per hora. Et qui huebre lo mendre lo ne salhen 2 sestiers per hora. Ajusta [a]quellas 3 summas que montan 9. Et digas: si 9 sestiers me venen de 1 hora, de quant me vendran 12 que te lo vayssell? Multiplica 12 que voles saber per 1^a hora, monta 12, partis per 9 que te eran vengutz de 1^a hora, que ne ve 1 et $\frac{3}{9}$, que valen $\frac{1}{3}$, et en 1^a hora et $\frac{1}{3}$ de hora se·n salhiria tot lo vi qui ne quitava totz los dosis en 1 colp.

Item 2 homes parteissen en 1 jorn & en una hora de 2 vilas, como per manuscrich: la eixemple lo 1 part de Beses que va a Barcilona et l'autre va de Barcilona a Beses. Et aquell que part de Beses fay lo cami en 7 jorns, et l'autre n'i met 9 jorns. Demandi en quant de temps se deven avistar al cami et quant aura caminat cada un d'els. Resposta: digas que lo hi aja de cami 63 legas. Aquell que fa lo cami en 7 jorns va cada dia 9 legas. Et aquell que fay lo camin en 9 jorns vay cada dia 7 legas. Ajusta aquellas 2 summas, que montan 16. Digas: si 16 me venen de 1 dia de quant me vendran 63 legas que es tot lo cami? Multiplica 63 que voles saber per 1 dia, monta 63, partis per 16 que ne ve 3 et $\frac{15}{16}$ et en 3 dias & $\frac{15}{16}$ de jorn se encontran.

Si voles saber quant aura caminat cascun, multiplica so que es vengut per las legas que caminavan & saubras ho.

Un merchant ha comprat 3 draps que costan 60 motos et non sap que costa lo premier, mas ell sab be que lo 2 costa lo doble del premier et lo 3 costa lo triple del 2. Demandi que costa cada un? Resposta: pausi que lo 1 costa 2, et lo 2, 4 et lo 3, 12. Ajusta aquellas 3 summas que montan 18. Et digas: si 18 me

venen de 2, de quant me vendran 60? Multiplica 60 que voles saber per 2 que as mes, que montan 120, partis per 18 que te eran vengutz de la positio, que ne ve 6 he $\frac{12}{18}$, que valen $\frac{2}{3}$. Et 6 motos & $\frac{2}{3}$ costa lo premier, lo 2 costa lo doble que es 13 & $\frac{1}{3}$, lo 3 costa lo triple del segont, monta 40, ajusta aquellas 3 summas et atrobaras 60. manuscrich: 8?

Item un boticari met 100 motos en 4 manieras de specias, so es [*] Probablament "grana de Paradis" (Amomum granum Paradisi) al gust de menta pebrada. pebre, gingibre, grana [*] & girofle, et non sap de segur que li costa cada una d'aquellas specias, mas ell sap que lo gingibre costa lo doble del pebre et la grana costa lo triple del pebre & lo girofle 4 vegadas tant como lo pebre. Demandi que costa cada una? Resposta: pausi que lo pebre coste 3 motos, lo gingibre 6, la grana coste 9, lo girofle 12. Ajusta ho tot, montan 30. Aras digas: si 30 me venen de 3, de quant me vendra 100? Multiplica 100 [*] que [*] manuscrich: 110 voles saber per 3 que as mes, montan 300,partis per 30, que eran vengutz de la positio, que ne ve 10, et tant val lo pebre, lo gingibre 20, la grana 30, lo girofle 40 & es feyt & aissi fenis [la] 1^a posicio.

Siec se la regla de 2 falsas positions ab sos exemples la qual es la es la

3 regla general mot meravilhosa de 2 falsas atrobar la veritat

Veire la version, fòrça similària, del Compendion de l'àbaco de F. Pellós, cap XVII, folio 67r [139] Aprop que yeu hey tractat de una positio falsa resta que yeu tracte de las 2 falsas positions, que la 3 regla general de la qual donarei diverses exemples et diverses ensenhamens segont que en diversas manieras servis affer diversas rasons mot defficils las quals far sens regla seria granda fatiga como demostrarem los exemples seguens.

nota que se deu
sustrayre
ho ajustar Plus et plus, mentz & mentz sustrahen, plus & mentz ajustant.

Per aquesta regla son de saber 4 causas. La premiera que en aquesta regla es, hom sustran ho ajustan 2 vegadas la premiera es per atrobar lo partidor. Et la 2 per atrobar la summa que se deu partir.

La premiera que es per atrobar lo partidor se fay tantost que las 2 falsas posicions son feytas, la 2 que es per atrobar la summa que se deu partir se faquant la multiplicacio de las 2 positions se fan en tal maniera que la premiera positio multiplica so que te ve de la 2, sie plus ho mentz. Et las 2 positio multiplica so que era vengut de la 1^a, si hi a estat plus o mentz. Et aixi aquellas multiplications se fan per maniera de crotz. Et per tal que hom veian miels la partida et la maniera com se deven

escriure, pausa 3 exemples segont las partidas de la regla.

Lo premier exemple.

Lo 2 exemple.

Lo 3 exemple.

Item deves saber segondament que per evitar prolixitat de paraullas que totas la respostas de las questions & rasons que se segueyssen yeu pausarey per la manieras que son pausas los exemples desus pausatz. 

Item mas es de saber que quant en la raso que se deura far, lo si nominaran 2 nombres determenatz per los quals vendran tant de gasanh & tant mais de gasanh o tant mais de perdoa o tant de perdoa per lo un et quant de gasanh per l’autre que hom deu metre un nombre en lo qual se atroban entirament aquells dus nombres prepausatz en la rason & deves saber que la major dona la perdoa & la menor dona lo gasanh.

Item quartament deves saber que totas las rasons que se poden fer per la 2 partida de 1^a falsa positio se deu

far per la regla de 2 falsas positions et non pas lo contrari et per so de present laissi las rasons feytas desus per la 2 partida de una positio las quals leugierament se poden applicar ad aquesta regla. Et las rasons que se sieguen et lurs senblans non se poden fer per una positio de las quals la premiera es.

Un merchant a comprat 3 pessas de drap que li costan 30 motos & non sap certanament que costa cada una de las 3 pessas, mas sab be que la 2 costa lo doble de la premiera & 4 plus, la 3 costa 3 vegadas tant com la 2 e 7 mens. Demandi que costa cada una. Resposta: pausi que la premiera coste 3, la 2^a coste 6 et 4 plus, monta 10. La 3 costa 3 vegadas 10, fan 30, mens 7, restan 23. Aras per saber si as atrobat ta rason, ajustas la 3 summas, que montan 36. Et tu non volias mas 30. Per so digas: per la premiera posicio, si 3 plus 6. Item per la 2 falsa positio met que la premiera costa 4, la 2 coste lo doble que es 8, et 4 plus fan 12, la 3 coste 3 vegadas 12 son 36, leva ne 7, restan 29, ajusta aquellas 3 summas que montan 45, et tu non volias sinon 30. Per so digas

per la 2 posicio per 4 plus 15. Aras car las 2 posicions son faytas et plus & plus sostrayon fay la premiera sustractio per atrobar lo partidor et leva lo plus de la premiera que es 6, del plus de la 2 que es 15. Resta 9 que es lo partidor. Item fay la 2 multiplications et premierament lo plus de la premiera que es 6 per la 2 positio que es 4. manuscrich: $\frac{4}{6}$ Et digas 4 vegadas 6 son 24. Item multiplica lo plus de la 2^a que es 15 per la premiera positio que es 3, et digas: 3 vegadas 15 son 45. Aras pueis que son feytas las multiplications, fey la 2^a substractio per atrobar la summa que deves partir, et leva 24 de 45, restan 21; partis 21 per 9, que ne ve 2 et $\frac{3}{9}$, que valen $\frac{1}{3}$, et 2 motos & $\frac{1}{3}$ de moto val la premiera pessa.

La 2^a costa lo doble & 4 de plus, que monta 8 et $\frac{2}{3}$.

La 3^a val 3 vegadas tant como la 2^a mens 7, que montan 19, et si ajustas aquellas 3 summas, atrobaras 30 motos que costavan & per aquesta maniera entendas de fer totas las seguens.

Item 1 merchant ha comprat 15 pessas de draps que son compradas a 9 et a 13 et costan totas 160 motos. Demandi

d’aquellas de 9 quantas n'i a et d'aquellas de 13. Resposta: pausi que n'i aja 12 d'aquellas de 9, per conseguent lo n'i a 3 d'aquellas de 13 e atrobaras mentz 13, que tu non voles. Item per la 2^a posicio pausa que n'i aja 10 d'aquellas de 9. Per conseguent lo n'i a 5 d'aquellas de 13, et atrobaras mentz 5 de tot lo per 135.

Et 9 & $\frac{6}{8}$ que no li [?] la 1^a.

Item 2 merchans venen de fiera la un ha 20 sacx de lana per los quals ell paga a la leuda 1 sac de la lana & lo leudier li torna 2 liuras & es be pagat. Lo 2 a 60 sacx de la [lana] per los quals ell paga al leudier 2 sacx de lana et 6 liuras plus. Demandi quant val lo sac de la lana et quant ha pagat de leuda per sac. Resposta: per saber las posicions pausa que lo sac valha 4 liuras, doncx paga ell 2 liuras per 20 sacx car [lo leudier] torna 2 liuras e per aquesta maniera quant los 20 pagan 2 liuras, los 60 sacx deven pagar 6 liuras, plus que son 12 liuras et per so paga trop [8] liuras, et es per 4 plus 8. Autrament pausa que lo sac valha 8 liuras, de las quals li torna 2 liuras, et aixi ell paga per 20 sacx 6 liuras et aquell que los 60 sacx,

manuscrich: 61 paga 2 sacx que valen 16 liuras & 6 plus que montan 22 liuras & ell no deuria pagar a la rason de l’autre si non 18 & aixi es per 8 plus 4.

Et 12 liuras val lo sac & paga 10 liuras per 20 sacx.

Item 1 merchant ha mes 20 liuras que son 200 souses en 2 manieras de blat, so es en froment & en civada, & ha comprat lo sestier del froment 10 souses et lo sestier de la civada ha comprat 5 souses. Aquell merchant retorna vendre son blat et vent lo sestier de la civada 4 souses & lo sestier del froment 12 souses, et atrobat de gasanh 10 souses. Demandi quantz sestiers del froment & quantz de la civada avia comprat e quant avia metut d’argent en lo cascun blat. Resposta: pausa que hi aja 10 sestiers de froment que valen 100 souses, resta que lo hi avia 20 sestiers de civada que valen 100 souses, torna los vendre a 12 & a 4, que montan 200 souses et tu volias 210. Per que es mentz 10 souses. Autramens pausa que hi avia 15 sestiers de froment que valen 150 souses. Resta

que no hi a si no 10 souses de civada que valen 50 souses. 10 × 12 + 20 × 4 = 200 + 10 = 210 Torna los vendre a 14 et a 4 com es dit, montan 220, que es plus 10 souses que non voles. Per que es per 15 plus 10.

Et 12 sestiers & $\frac{1}{2}$ de froment avia comprat que valian 125 souses & 15 de civada que valen 75 souses, torna los vendre com es dit & atrobaras 210 souses.

Item 1 merchant vol comprar 1 quintal de cera & atroba la cera nova per 14 motons et la cera vielha per 9 motons, & ell non vol despendre si non 11 motons e vol aver 1 quintal de cera, mesclant la nova ab la vielha. Demandi quant deu aver de cada una & quant metra d’argent en cascuna a complir qu'ell aja 1 quintal de cera et que non despenda mas 11 motons. Resposta: que pausi que prenga 20 liuras [de pes] de la cera nova que valen 2 motons & $\frac{4}{5}$ & senblantment ell pren 80 liuras de la cera vielha que valen 7 motons & $\frac{1}{5}$. Ajusta aquellas 2 summas, montan 10 & es: per 20 mens 10.

Autrament, pausi que ell prenga 60 liuras de la cera nova

que valen 8 motons & $\frac{2}{5}$, per conseguent ell pren 40 liuras de la cera vielha que valen 3 motons & $\frac{3}{5}$. Ajusta aquellas summas que montan 12 et aixi es: per 60 plus 1

Et 40 liuras de cera nova ha pres que valen 5 motons & $\frac{3}{5}$, et 60 liuras de la vielha que valen 5 motons & $\frac{2}{5}$.

Nota las 2 rasons seguens per baratar. 2 merchants volen baratar ensemps, so es que volen cambiar lurs mercadaries ensemps & la un dels ha lana et l’autre ha draps. Aquell que ha draps vol de la canna 24 souses a baratar que non val per bona merchandisa si [non] 20 souses. Demandi que li demandi que li deu vendre l’autre lo quintal de la lana que non val si non 12 liuras a so qu'ell non perda. Resposta: per la regla de [3], que es plus breu, digas: si 20 que val lo drap montan de 4, de quant montaran 12 que val [la] lana? Multiplica 12 que voles saber per 4, montan 48, partis per 20 que val lo drap, que ne ve 2 liuras & $\frac{8}{20}$, que vale 8 souses et 2 liuras et 8 souses deu cargar sa lana et

aixi ve lo quintal 14 liuras et 8 souses.

Autramentz, per 2 falsas posicions, premierament sapias quantas cannas del drap valen lo quintal de la lana & per saber ho, partis 12 liuras que val lo quintal de la lana per 20 souses que val la canna del drap, encarestis son drap que trobaras que ne ve 12, & car aquell del drap encarestis son drap de 2 souses per canna, aquell de la lana, si layssa lo quintal per 12 liuras, ell pert la valor de 2 cannas que es 2 liuras de moneda. Car ell non vendría lo quintal si non a rason de 10 liuras. Per so demandi de quant deu cargar sa lana asso que non perda. Resposta: si ell carga lo quintal de 3 liuras so es que de 12 fassa 15, trobaras que ell decep son companho de [$\frac{1}{2}$ liura] que son [10] souses et es per [3] plus $\frac{1}{2}$. Item si ell carga lo quintal de 4 liuras so es que de 12 fassa 16, ell decep son companho de 1 liura et $\frac{8}{24}$ que valen $\frac{1}{3}$ et es per 4 plus 1 & [$\frac{1}{3}$]

Et de 2 liuras & $\frac{2}{5}$ de liura que valen 8 souses deu cargar lo quintal de la lana.

Dus merchants son que volen baratar

ensemps, lo 1 a draps et l’autre ha lana.

Et aquell que ha los draps vol de la canna 24 souses que non val si non 20 souses, e vol $\frac{1}{2}$ en argent. Demandi de quant deu carcar aquell de la lana lo quintal que non val que 12 liuras asso que ell non perda, bayllant la mittat en argent e l’autra $\frac{1}{2}$ en lana.

Nota aquesta resposta special. Premierament tu deves fer ta rason engoal per la regla premiera desus. Aprop regardar quina partida demanda aver en argent so es si vol la $\frac{1}{2}$ o lo $\frac{1}{3}$ o lo $\frac{1}{4}$. Et aixi de las autras partidas. Si demanda la mittat, tu deves manuscrich: quart metre lo doble del carc que fa engoalar los merchandias. Et si demanda lo $\frac{1}{3}$, ell manuscrich: $\frac{1}{4}$ li deu mais ajustar la $\frac{1}{2}$ del carc. Et si vol aver lo $\frac{1}{4}$, ell deu mais ajustar lo manuscrich: $\frac{1}{4}$ $\frac{1}{3}$ del carc & aixi totztemps ajustar hi la partida que vol mais plus propdana que ell demanda.

Exemple en la rason feyta ell deu cargar la lana de 2 liuras et 8 souses, dobla ho, son 4 liuras 16 souses et aixi li deu vendre lo quintal 16 liuras et 16 souses et vendra a son propaus. Et si agossa demandat lo $\frac{1}{3}$ del argent, ell agra ajustat la mittat de 2 liuras & 8 souses que es 1 liura & 4 souses et agra montat lo quintal 15 liuras et

12 souses. Et si agues demandat lo $\frac{1}{4}$ en argent, ell agra ajustat lo tertz & 2 manuscrich: la mittat liuras & 8 souses que es 16 souses & agra montat lo quintal 15 liuras et 4 souses. Et aixi o entendas de totas las autras partidas per la qual raso se fa, ho se pot fer per 2 falsas positions mas que es trop enpachat et aquesta practica es plus breva per que layssi la de fer per 2 falsas positions.

Item 1 merchant ha comprat de blat 5 sestiers per 3 motos et a ne tant comprat que lo nombre dels sestiers del blat ajustat ab lo nombre dels motos que hi a metutz non montan sinon 60. Demandi quantz motos hi a ni quantz sestiers de blat. Resposta: pausi que lo hi aja 3 motos et hi aja 5 sestiers de blat, ajusta ho tot ensemps, montan 8, ad annar entro a 60, falhen 52, et es per 3, mens 52. Item pausi que lo hi aja 6 motos, lo hi a 10 sestiers de blat, ajusta ho tot ensemps, montan 16, ad annar entro 60 ha 44, et es per 6, mens 44.

Et 22 motons & $\frac{4}{8}$ que valen $\frac{1}{2}$ moto hi a, manuscrich: 2

et lo romanent que es entro a 60 que monta 37 & $\frac{1}{2}$ son lo[s] sestiers del blat.

Item 1 home te tant de boyers et ha tant d’argent en sa borsa que si ell dona a cada un 4 souses, lo li·n sobran 20 souses. Et si ell dona a cascun 5 souses, lo li·n falhirien 10 souses a pagar totz los boyers. Demandi quantz boyers ha ni quant d’argent ha. Resposta: pausi que ell aja 10 boyers a 4 souses, montan 40 & 20 que li·n restan, son 60 souses que ell ha et si ell ne dona 5 souses deven montar 70 car lo li·n deven defalhir 10, & non montan si non 50, que es per 10 mens 20. Item pausi qu’ell aja 20 homes a 4 souses, montan 80, et 20 que li·n sobran, son 100 souses que ell ha. Et si dona 5 souses lo li·n falhiran 10, et non montan si non 100, Per que es per 20 mens 10.

Et 30 homes ha que montan a 4 souses & 120 et 2 que li·n restan son 140 souses que ell ha per manuscrich: defafalhrien que li defalhirien 10 souses si dona 5 souses a cada um.

Item 1 home intra en fiera, et lo premier jorn dobla tot son argent et despent 1 gros. Item lo 2 [jorn] tripla tot son argent que li era restat et despent 2 * manuscrich: qudrupla gros. Item lo 3 jorn quadrupla* son argent

que li era restat & despent 2 gros, et troba qu’ell no ha si non 3 gros. Demandi quant portava d’argent. Resposta: pausi que manuscrich: 1 gros et $\frac{1}{2}$ ell porta 1 gros, lo dobla son 2 gros et despent 1 gros, resta li 1 gros, lo qual tripla e son 3 gros & despent 2 gros res[ta] li·n 1, lo qual quadrupla et son 4 gros, dels quals ne despent 2 et restan li·n autres 2 et ell ne volia 3 per que es per 1 mens.

Item pausi qu’ell portes 2 gros, & ell los dobla son 4, & ell ne despent 1, restan son 3 gros, los quals tripla, son 9, et despent ne 2, restan 7, lo quals quadrupla, son 28, et ne despent 2, restan li·n 26, et ell no ne volia si non 3. Per que es [per] 2 plus 23. manuscrich: 3

$\frac{1}{24}$ et 1 gros portava.

Item 1 revendedor ha comprat tant de pomas et hi a tant mais d’argent que si ell las revent 5 per 1 blanc contant a 5 deniers, ell gasanha 6 deniers et si ell non ne dona si non 4, ell gasanha 12 deniers. Demandi quantas pomas ha comprat et quant hi a metut d’argent. Resposta: pausi que ell aja 20 pomas si ell las vent 5 al blanc, ell ne fa 20 deniers et gasanha 6 deniers. Per que no li costan si

si no 14 deniers & si ell la revent 4 al blanc, ell ne fa 25 deniers, et deurie ne far 26. Per que es per 20 mens 1. Item pausi que ell agues 40 pomas & la revent 5 a la blanca, ell ne fay 40 deniers et hi gasanha 6 deniers, per so non li costan mas 34 deniers. Et si ell las revent 4 a la blanca, ell ne fay 50 deniers et non en deurie far si non 46 deniers que es lo principal et 12 de gasanh per que es per 40 plus 4.

Et 24 pomas ha comprat que li costan 18 deniers per que valen 30 qui las vent 4 a la blanca.

Un autre revendedor ha comprat tant de huous & hi a tant metut d’argent que si ell los revent 5 al blan[c], ell hi pert 6 deniers. Et si ell los revent 4 al blanc, ell hi gasanha 12 deniers. Demandi quantas huous ha comprat et quant hi a metut d’argent. Resposta: pausi que ell aja 20 huous, si ell los revent 5 al blanc ell ne fan 20 deniers et ell hi pert 6 deniers, per que li costan 26 deniers. Et si ell los revent 4 al blanc, ell ne fay 5 blancx que son 25 deniers, et deurien esser 38 deniers, que son 12 plus de 26, que costavan.

Per que es per 20 mens 13. Item pausi que ell aja 40 huous; si ell los revent 5 al blanc, [*] que hi pert;
costan li doncas
40 deniers & si
ell los revent 4
al blanc, ell ne
fay 10 blanx
que son 50 deniers. ell ne fay 40 blancx e 6 deniers [*] et ell ne devia far 58, que son 12 plus que costavan. Per que es per 40 mens 8.

Et a 72 huous avia comprat que costavan 78 deniers.

Item 4 huous mens 2 deniers valen 7 deniers he 1 huou plus. Demandi quant val 1 huou. Resposta: pausi que valha 2 deniers, montan 8, leva ne 2 deniers, restan 6 deniers & devia restar 7 deniers et 1 huou plus que val 2 deniers, per que es per 2 mens 3. Item pausi que lo huou valha 4 deniers, montan 16 deniers, leva ne 2 deniers, restan 14 deniers, et no devian restar que 7 et 1 huou, que son 4 deniers, que son 7 et et 4 montan 11 et nos avem 14 per que es per 4 plus 3.

Et 3 deniers val 1 huou.

Item 1 revendor compra 12 deniers de pomas et de peras, et compra las pomas 8 per 1 denier. Et de las peras 6 per 1 denier; et torna las revendre & vent las pomas 9 per

1 denier. Et non remens las peras 8 li costavan 1 denier las peras que ell a comprat 6 per 1 denier et las vent 5 per 1 denier et troba que ell gasanha 1 denier. Demandi quantas pomas et quantas peras ha comprat & quant ha metut d’argent en cada una de las fruytas. Resposta: pausi que ell aja mes 6 deniers en pomas que montan 6 vegadas 8, que son 48. Et torna las revendre 9 per 1 denier, de ne ven a 5 deniers & $\frac{3}{9}$, que valen $\frac{1}{3}$. De peras a comprat a 6 deniers, que montan 36 deniers et torna las revendre a 5 per 1 denier que venen a 7 deniers & $\frac{1}{5}$. Ajusta ho tot, montan 12 deniers et $\frac{8}{15}$, et devia montar 13 deniers per 1 que devia gasanhar; per que es per 6 mens $\frac{7}{15}$. Item pausi ell ha conprat a 8 deniers de pomas que montan 8 vegadas 8, son 64, et torna las vendre, dona ne 9 per 1 denier, et fan 7 deniers & $\frac{1}{9}$, et de peras ha comprat a 4 deniers, que montan 4 vegadas 6, que son 24 et torna las vendre, dona ne 5 per 1 denier, que fan 4 deniers & $\frac{4}{5}$. Ajusta ho tot, monta 11 deniers et $\frac{41}{45}$ et aixi es per 8 mens 1 et $\frac{4}{45}$.

Et 4 deniers et $\frac{210}{420}$ que valen $\frac{1}{2}$ ha mes en

pomas et ne ha agut 36 et torna las revendre et dona ne 9 per 1 denier, et fay ne 4 deniers. Et en peras ha mes 7 deniers & $\frac{1}{2}$ denier et ne agut 45 et torna las revendre et no ne dona mas 5 per 1 denier et fay 9 deniers. Ajusta manuscrich: ha
iusta 9 deniers et 4 que son 13 et aissi gasanha 1 denier.

Item 1 revendor compra 60 pomas que li costan 24 deniers et torna las revendre et dona ne aytant segont proporcio per 1 denier como ell avia comprat et gasanha 1 denier. Demandi com las ha vendudas. Resposta: quant ell ha comprat 60 pomas per 24 deniers, ell ha per 1 denier 2 pomas & $\frac{1}{2}$, que son 5 pomas per 2 deniers. Aras pausi que venda 20 pomas, donant ne 2 per 1 denier, ell ne fay 10 deniers, et resta que ell deu vendre 40 pomas, donant 3 per 1 denier, montan 13 deniers & $\frac{1}{3}$, et aquesta ab los 10, montant 23 & $\frac{1}{3}$, et per 20 mens 1 et $\frac{2}{3}$ que defalh ad anar a 25 per gasanhar 1 denier. Item pausi que ell venda 40 pomas donant ne 2 per 1 denier, ell ne fay 20 deniers. Et aprop ell ne vent 20 donant ne 3 per 1 denier, que ne fay 6 deniers & $\frac{2}{3}$. Ajusta tot, monta 26 & $\frac{2}{3}$, que es plus de 25 deniers [de] 1 & $\frac{2}{3}$, per que es per 40 plus 1 & $\frac{2}{3}$.

manuscrich: 1 doblidat, e $\frac{\mathrm{x}}{3}$ suprimits

Et 30 pomas ha vendut donant ne 2 per 1 denier. Aprop ha vendut las autras 30 donan ne 3 per 1 denier, que valen 10 deniers, et aixi ell las vent donant ne 5 per 2 deniers et gasanha [?].

Item 1 revendedor ha de pomas, de manuscrich: $\frac{1}{2}$ las quals ell vent la mittat a 1 persona e li·n dona [1^a] d'avantage. Item torna vendre $\frac{1}{2}$, la mittat d'aquellas que li son restadas a una autra persona et li·n dona 1^a d'avantage. Item autra vegada torna manuscrich: $\frac{1}{3}$ vendre lo $\frac{1}{2}$ d’aquellas que li son romasas a 1^a autra persona & li·n dona una d'avantage et derrierament li·n restan 3. Demandi quantas pomas avia qu’ell aja feytas aquellas vendas sens partir denguna poma per mieg.

Resposta:

los nombres en verd son multiplicats per 2 (las pomas non se partisson per mieg?) et 38 pomas avia.

Per autra practica plus presta a fer senblans rasons & per restar tantas pomas com tu voldras, te doni tala regla.

Tu deves acomensar a las pomas que voles que romangan de doblar.

Et doblar tantas vegadas com sera propausat de partir las per $\frac{1}{2}$. Et sobre cascun

doblar 1 mais que per $\frac{1}{2}$, voli ajustar 2, per 2 ajustariam 4, et [per] 3, ajustaríam 6, et cetera, et $\frac{1}{2}$ ajustaria 1, &cetera. Eyxemple: en la rason feyta, dobla 3 que voles que resten, son 6; ajusta 2 per lo 1 que dona mais que per mieg, son 8. Item dobla 8, son 16; ajusta 2, son 18. Item dobla 18, son 36; ajusta 2, son 38. Et aissi faras de totas las autras senblans, retenen be que 1 vol dire 2, sobre cascun doblar.

Son 2 homes que an tant d’argent que lo premier ditz al 2: dona me 1 denier dels tieus et yeu aurey ne autans como tu. Et lo 2 respon mas me•n dona tu 1 dels tieus & yeu ne aurey lo doble mais que tu. Demandi quant ha d’argent cascun. Resposta: pausi que lo premier aja 3 deniers, es mestier que lo 2 ne aja 5. Quant ell li·n dona 1, lo cascun ne aura 4, et seran engoals; si lo premier ne dona 1 al 2, lo 2 ne aura 6, et non ne devia aver si non 4 que es lo doble del premier. Per que es per 3 plus 2. Item pausi que lo premier aja 4 deniers; per conseguent lo 2 ne deu aver 6; si ell li·n dona 1 lo cascun ne aura 5, et seran engoals. Et si lo premie[r] ne dona 1 al 2, ell ne aura 7, et non en devia

si non 6, que es lo doble de 3, que restan al premier. Per so es per 4 plus 1.

Et 5 ha lo premier, per conseguent lo 2 a 7.

Item son 2 homes que an tant d’argent que lo 1 di al 2: dona me 1 de tos deniers et yeu ne auriey 2 vegadas tant como tu. Et respon lo 2 ditz mas me dona 1 denier dels tiens, yeu ne aurey 4 vegadas tant como tu. Demandi quant d’argent aura cada un. Resposta: pausi que lo premier aja 5 deniers, lo 2 ne deu aver asso que quant ell li aura bayllat 1 denier, que ell aja lo doble 4 vegadas per so car ell li·n bayla 1 ell ne ha 6. Et lo segont non n'a mas 3. Et si lo premier ne baylla 1 al 2, lo 2 ne aura 5, et deuria ne aver 16, que es 4 vegadas 4, que restavan al premier. Per que es per 5 mens 11. Item pausi que lo 1 aja 7 deniers. Lo 2 ne deu aver 5, asso que quant ell li·n aura bayllat 11, qu'ell aja lo doble que son 8, et ell non aura que 4. Et si lo premier baylla 1 denier al 2 lo cascun dels ne auran

6. Et lo 2 ne deurie aver 4 vegadas 6, que son 24, per que es per 7 mens 18.

manuscrich: 27

manuscrich: 3 deniers et $\frac{6}{7}$ ha lo 1
et lo 2 ha 2 deniers & $\frac{2}{7}$ Et 1 denier et $\frac{6}{7}$ de denier ha lo 1 et lo 2 ha 2 deniers et $\frac{3}{7}$.

Son 3 homes que an tant d’argent que lo 1 ditz al 2: dona me 1 denier dels tieus & yeu ne aurei aytant como tu. Et dis lo 2 al 3: dona me 1 dels tieus deniers et yeu ne aurey 2 vegadas tant como tu. Et dis lo 3 al premier: dona me 1 de tos deniers et yeu ne aurey 3 vegadas tant como tu. Demandi quant d‘argent ay lo cascun d’els. Resposta: pausi que lo 1 aja 3 deniers; lo 2 ne deu aver 5, asso que quant ell li·n aura donat 1, que ells sien engoals; lo 3 ne deu aver 4, asso que quant ell ne aura donat 1 al 2, que lo 2 ne aja lo doble del tertz. Aras vejan si lo premier ne dona 1 al 3, si lo tertz ne aura 3 vegadas tant como lo premier ell ne aura 5, et devia ne aver 6 per que es per 3 mens 1. Item pausi que lo premier aja 5 deniers; lo 2 ne deu aver

7, per tal que quant ell ne aura donat 1 al premier, els deven esser engoals et lo 3 ne deu aver 5, asso que quant ell ne aura donat 1 al 2, que lo 2 ne aja lo doble. Aras si lo 1 dona 1 denier al 3, si lo 3 aura 3 vegadas tant como lo 1, ell ne aura 6 et non en devia aver si non 3 vegadas 4, que restan al premier, que son 12 et es per 5 mens 6.

Et 2 deniers et $\frac{3}{5}$ ha lo 1, et lo 2 ne ha 4 $\frac{3}{5}$ et lo 3 ne ha 3 et $\frac{4}{5}$ & es feyta la rason.

Et aissi appar que la regla de [2] falsas positions se aplican en diversas manieras et an diversas et difficils questions; las quals reglas de present abasten los eyxemples desus pausas. Car per aquells hom pot veser la maniera com se aplican & la maniera com se·n pot hom ajudar.

Siec se la 4 regla & la derriera general que se appella regla de appositio et remotio, sens la practica, car non es trop util ni aprofitabla.

Et per donar fi et conclusio al libre hutil et

profitabla a merchans.

Quant hom ha mais que hom non vol hom deu levar de so que fa montar & creysser so que fa abayssar. Et quant hom ha mens que hom non vol, hom deu levar de so que que fay abayssar et metre de so que fa creysser, metent et levant entro que hom venga a son prepaus de so que hom vol.

Per aquesta regla deves saber que propriament lo non es regla mas un avisament per far las questions que non se poden far per veraya regla. Et per so n’ey feyta regla, per so que qui s’en saura ajudar serva & gauda de major pena de la qual darey alcuns eyxemples en questions et respostas sens la practica de la regla car serie trop lonc. Car lo es necessari que l’ajustament del home hi ajude & hi servisca car autrament non se poyrie far.

Son 12 personas entre homes & femnas et petitz enfantz que han 12 deniers a partir; los homes an 2 deniers et las femnas ne an 1 et los enfantz ne an $\frac{1}{2}$. Demandi quantas femnas son, ni quantis homes et quantz enfantz. Resposta: son 2 homes, 6 femnas et 4 petitz enfantz.

manuscrich: portat Son 3 fe[m]nas que portan al mercat de pomas a vendre; la 1^a ne porta 50 et l’autra 30 et l’autra 10. Et venden las en tal maniera que aytant ha d’argent la una como l’autra. Demandi com las an vendudas. Resposta: vendent las. Ellas las venden a 2 pres: 7 per 1 denier et 1 per 3 deniers. Et aixi cada una ne porta 10 deniers. Car la premiera ne vent 49 a 7 per 1 denier, aprop ne vent 3 per 1 denier et son 10 deniers. La 2 ne vent 28 a 7 per 1 denier que son 4 deniers, aprop ne vent 2 per 6 deniers, e son 10 deniers. Et l’autra ne vent 7 per 1 denier, aprop 3 a 3 deniers, son 9 deniers et 1 denier que tenie et son 10 deniers.

Et si venden a 3 pretz: 8 per 1 denier, et 1 & $\frac{1}{2}$ per 1 denier et 2 per 1 denier. La premiera al premier [pretz] ne vent 48 que valen 6 deniers, en lo segont [pretz]: 1 & $\frac{1}{2}$, manuscrich: En lo tertz… qual que valen 1 denier, en lo tertz [pretz] qual [e] 2 que val 1 denier, et son 8 deniers que has feyt de sas pomas. La 2 ne vent al premier pretz 24 que valen 3 deniers. En lo segont [pretz] 5 & $\frac{1}{4}$, que valen 1 denier et $\frac{5}{2}$. Et al tertz [pretz] $\frac{3}{4}$ que valen 1 denier et $\frac{1}{2}$. Et son 8 deniers. La terza ne vent al premier 4, que valen $\frac{1}{2}$ denier, al segont [pretz] 3 & $\frac{3}{8}$ que valen 2 deniers et $\frac{1}{4}$, al terz [pretz: 2 et $\frac{5}{8}$] que ne ve 2 et $\frac{5}{8}$ que valen 5 deniers et $\frac{1}{2}$, monta tot 8 deniers. Et aissi cada una de las donnas a 2 pretz fan 10 deniers et a 3 pretz ne fan 8.

Item 1 merchant compra 30 cannas de drap que costan 30 motos. Et n'i a de 4 motos et de 2 motos et d'autres de $\frac{1}{2}$ moto. Demandi quantas n'i a de cascunas. Resposta: lo hi a 3 cannas de 4 motos que valen 12 motos et n'i a 3 de 2 motos que valen 6 motos et n'i a 24 de $\frac{1}{2}$ moto que valen 12 motos. Et aissi hi a 30 cannas et 30 motos. Et aissi fenis lo present libre de la sciencia de arismatica vulgarment dit algorisme.

Deo gratias, amen.

Finito libro sit laus gloria Christo.